101. Two bodies of masres $$1\,kg$$ and $$3\,kg$$ have position vectors $$\hat i + 2\hat j + \hat k$$ and $$ - 3\hat i - 2\hat j + \hat k,$$ respectively. The centre of mass of this system has a position vector
A
$$ - 2\hat i + 2\hat k$$
B
$$ - 2\hat i - \hat j + \hat k$$
C
$$2\hat i - \hat j - 2\hat k$$
D
$$ - \hat i + \hat j + \hat k$$
Answer :
$$ - 2\hat i - \hat j + \hat k$$
102. A light rod of length $$l$$ has two masses $${m_1}$$ and $${m_2}$$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
A
$$\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}{l^2}$$
B
$$\frac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}{l^2}$$
C
$$\left( {{m_1} + {m_2}} \right){l^2}$$
D
$$\sqrt {{m_1}{m_2}} {l^2}$$
Answer :
$$\frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}{l^2}$$
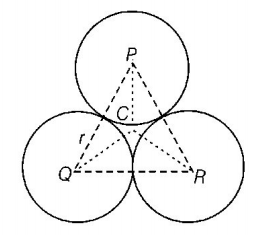
103. Three identical metal balls each of radius $$r$$ are placed touching each other on a horizontal surface such that an equilateral triangle is formed with centres of three balls joined. The centre of mass of the system is located at
A
horizontal surface
B
centre of one of the balls
C
line joining the centres of any two balls
D
point of intersection of the medians
Answer :
point of intersection of the medians
104. The moment of inertia of a disc of mass $$M$$ and radius $$R$$ about a tangent to its rim in its plane is
A
$$\frac{2}{3}M{R^2}$$
B
$$\frac{3}{2}M{R^2}$$
C
$$\frac{4}{5}M{R^2}$$
D
$$\frac{5}{4}M{R^2}$$
Answer :
$$\frac{5}{4}M{R^2}$$
105. A round disc of moment of inertia $${I_2}$$ about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia $${I_1}$$ rotating with an angular velocity $$\omega $$ about the same axis. The final angular velocity of the combination of discs is
A
$$\frac{{\left( {{I_1} + {I_2}} \right)\omega }}{{{I_1}}}$$
B
$$\frac{{{I_2}\omega }}{{{I_1} + {I_2}}}$$
C
$$\omega $$
D
$$\frac{{{I_1}\omega }}{{{I_1} + {I_2}}}$$
Answer :
$$\frac{{{I_1}\omega }}{{{I_1} + {I_2}}}$$
106. A particle moves in a circle of radius $$5\,cm$$ with constant speed and time period $$0.2\pi s.$$ The acceleration of the particle is
A
$$25\,m/{s^2}$$
B
$$36\,m/{s^2}$$
C
$$5\,m/{s^2}$$
D
$$15\,m/{s^2}$$
Answer :
$$5\,m/{s^2}$$
107.
With $$O$$ as the origin of the coordinate axis, the $$X$$ and $$Y$$-coordinates of the centre of mass of the system of particles shown in the figure may be given as. Here $$m$$ and $$2\,m$$ represent the masses of the particles.
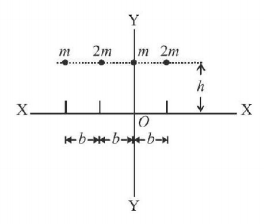
A
$$\left( { - \frac{b}{2},0} \right)$$
B
$$\left( { - \frac{b}{2},b} \right)$$
C
$$\left( { - \frac{b}{3},b} \right)$$
D
$$\left( { - \frac{2}{5}b,b} \right)$$
Answer :
$$\left( { - \frac{b}{3},b} \right)$$
108. Consider a thin uniform square sheet made of a rigid material. If its side is $$'a'$$ mass $$m$$ and moment of inertia $$I$$ about one of its diagonals, then
A
$$I > \frac{{m{a^2}}}{{12}}$$
B
$$\frac{{m{a^2}}}{{24}} < I < \frac{{m{a^2}}}{{12}}$$
C
$$I = \frac{{m{a^2}}}{{24}}$$
D
$$I = \frac{{m{a^2}}}{{12}}$$
Answer :
$$I = \frac{{m{a^2}}}{{12}}$$
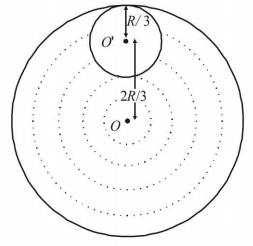
109.
From a circular disc of radius $$R$$ and mass $$9\,M,$$ a small disc of radius $$\frac{R}{3}$$ is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through $$O$$ is

A
$$4M{R^2}$$
B
$$\frac{{40}}{9}M{R^2}$$
C
$$10M{R^2}$$
D
$$\frac{{37}}{9}M{R^2}$$
Answer :
$$4M{R^2}$$
110. Consider a uniform square plate of side $$'a'$$ and mass $$'m'.$$ The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is
A
$$\frac{5}{6}m{a^2}$$
B
$$\frac{1}{{12}}m{a^2}$$
C
$$\frac{7}{{12}}m{a^2}$$
D
$$\frac{2}{3}m{a^2}$$
Answer :
$$\frac{2}{3}m{a^2}$$