181.
A beam of light consisting of red, green and blue colours is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.
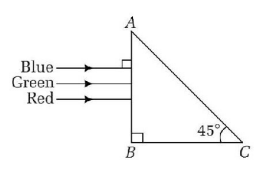
The prism will
A
separate the blue colour part from the red and green colours
B
separate all the three colours from one another
C
not separate the three colours at all
D
separate the red colour part from the green and blue colours
Answer :
separate the red colour part from the green and blue colours
182.
A container is filled with water $$\left( {\mu = 1.33} \right)$$ upto a height of $$33.25\,cm.$$ A concave mirror is placed $$15\,cm$$ above the water level and the image of an object placed at the bottom is formed $$25\,cm$$ below the water level. Focal length of the mirror is
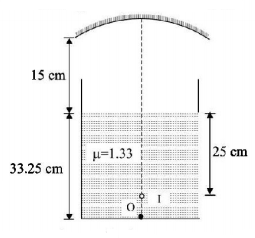
A
$$15\,cm$$
B
$$20\,cm$$
C
$$-18.31\,cm$$
D
$$10\,cm$$
Answer :
$$-18.31\,cm$$
183. The refractive index of a glass is 1.520 for red light and 1.525 for blue light. Let $${D_1}$$ and $${D_2}$$ be angles of minimum deviation for red and blue light respectively in a prism of this glass. Then,
A
$${D_1} < {D_2}$$
B
$${D_1} = {D_2}$$
C
$${D_1}$$ can be less than or greater than $${D_2}$$ depending upon the angle of prism
D
$${D_1} > {D_2}$$
Answer :
$${D_1} < {D_2}$$
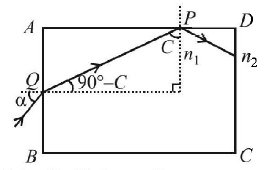
184.
A rectangular glass slab $$ABCD$$ of refractive index $$n,$$ is immersed in water of refractive index $${n_2}\left( {{n_1} > {n_2}} \right).$$ A ray of light is incident at the surface $$AB$$ of the slab as shown. The maximum value of the angle of incidence $${\alpha _{\max }}$$ such that the ray comes out only from the other surface $$CD$$ is given by

A
$${\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right)} \right]$$
B
$${\sin ^{ - 1}}\left[ {{n_1}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{1}{{{n_2}}}} \right)} \right)} \right]$$
C
$${\sin ^{ - 1}}\left( {\frac{{{n_1}}}{{{n_2}}}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)$$
Answer :
$${\sin ^{ - 1}}\left[ {\frac{{{n_1}}}{{{n_2}}}\cos \left( {{{\sin }^{ - 1}}\left( {\frac{{{n_2}}}{{{n_1}}}} \right)} \right)} \right]$$
185. A thin convex lens made from crown glass $$\left( {\mu = \frac{3}{2}} \right)$$ has focal length $$f.$$ When it is measured in two different liquids having refractive indices $$\frac{4}{3}$$ and $$\frac{5}{3}$$ it has the focal lengths $${f_1}$$ and $${f_1}$$ respectively. The correct relation between the focal lengths is:
A
$${f_1} = {f_2} < f$$
B
$${f_1} < f$$ and $${f_2}$$ becomes negative
C
$${f_2} < f$$ and $${f_1}$$ becomes negative
D
$${f_1}$$ and $${f_2}$$ both become negative
Answer :
$${f_1} < f$$ and $${f_2}$$ becomes negative
186. In a diffraction pattern due to a single slit of width $$a,$$ the first minimum is observed at an angle $${30^ \circ }$$ when light of wavelength $$5000\,\mathop {\text{A}}\limits^ \circ $$ is incident on the slit. The first secondary maximum is observed at an angle of
A
$${\sin ^{ - 1}}\left( {\frac{2}{3}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{1}{2}} \right)$$
C
$${\sin ^{ - 1}}\left( {\frac{3}{4}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{1}{4}} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\frac{3}{4}} \right)$$
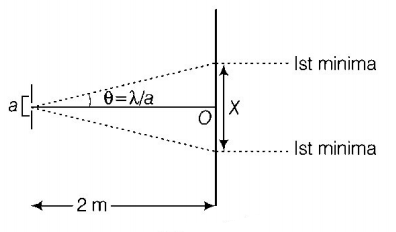
187. A beam of light of $$\lambda = 600\,nm$$ from a distant source falls on a single slit $$1\,mm$$ wide and the resulting diffraction pattern is observed on a screen $$2\,m$$ away. The distance between first dark fringes on either side of the central bright fringe is
A
$$1.2\,cm$$
B
$$1.2\,mm$$
C
$$2.4\,cm$$
D
$$2.4\,mm$$
Answer :
$$2.4\,mm$$
188.
A equilateral prism is made of a transparent material of refractive index $$\sqrt 2 .$$ A ray of light $$AB$$ is incident at $${45^ \circ }$$ as shown. The net deviation in the path of ray when it comes out of prism is
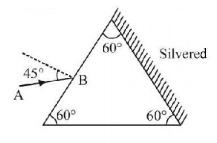
A
$${135^ \circ }$$
B
$${120^ \circ }$$
C
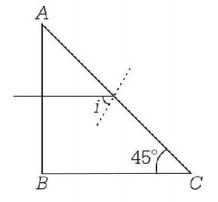
$${30^ \circ }$$
D
$${150^ \circ }$$
Answer :
$${150^ \circ }$$
189. $$I$$ is the image of a point object $$O$$ formed by spherical mirror, then which of the following statement is incorrect? (Take real or virtual objects at finite distances from pole)
A
If $$O$$ and $$I$$ are on the same side of the principal axis, then they have to be on opposite sides of the mirror
B
If $$O$$ and $$I$$ are on opposite sides of the principal axis, then they have to be on same side of the mirror
C
If $$O$$ and $$I$$ are on opposite sides of the principal axis, then they have to be on opposite sides of the mirror as well
D
If $$O$$ is on principal axis, then has to lie on principal axis only
Answer :
If $$O$$ and $$I$$ are on opposite sides of the principal axis, then they have to be on opposite sides of the mirror as well
190. In a compound microscope, the intermediate image is
A
virtual, erect and magnified
B
real, erect and magnified
C
real, inverted and magnified
D
virtual, erect and reduced
Answer :
real, inverted and magnified