211. A beam of light from a source $$L$$ is incident normally on a plane mirror fixed at a certain distance $$x$$ from the source. The beam is reflected back as a spot on a scale placed just above the source $$L.$$ When the mirror is rotated through a small angle $$\theta ,$$ the spot of the light is found to move through a distance $$y$$ on the scale. The angle $$\theta $$ is given by
A
$$\frac{y}{{2x}}$$
B
$$\frac{y}{x}$$
C
$$\frac{x}{{2y}}$$
D
$$\frac{x}{y}$$
Answer :
$$\frac{y}{{2x}}$$
212.
A transparent sphere of radius $$R$$ has a cavity of radius $$\frac{R}{2}$$ as shown in figure. Find the refractive index of the sphere if a parallel beam of light falling on left surface focuses at point $$P.$$
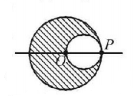
A
$$\mu = \frac{{3 + \sqrt 5 }}{2}$$
B
$$\mu = \frac{{3 - \sqrt 5 }}{2}$$
C
$$\mu = 3 + \sqrt 5 $$
D
$$\mu = \frac{{1 + \sqrt 5 }}{2}$$
Answer :
$$\mu = \frac{{3 + \sqrt 5 }}{2}$$
213.
$$r$$ and $$r’$$ denote the angles inside an equilateral prism, as usual, in degrees. Consider that during some time interval from $$t = 0$$ to $$t = t,r’$$ varies with time as $$r' = 10 + {t^2}.$$ During this time $$r$$ will vary as (assume that $$r$$ and $$r’$$ are in degree)

A
$$50 - {t^2}$$
B
$$50 + {t^2}$$
C
$$60 - {t^2}$$
D
$$60 + {t^2}$$
Answer :
$$50 - {t^2}$$
214. Two polaroids $${P_1}$$ and $${P_2}$$ are placed with their axis perpendicular to each other. Unpolarised light $${I_0}$$ is incident on $${P_1}.$$ A third polaroid $${P_3}$$ is kept in between $${P_1}$$ and $${P_2}$$ such that its axis makes an angle $${45^ \circ }$$ with that of $${P_1}.$$ The intensity of transmitted light through $${P_2}$$ is
A
$$\frac{{{I_0}}}{2}$$
B
$$\frac{{{I_0}}}{4}$$
C
$$\frac{{{I_0}}}{8}$$
D
$$\frac{{{I_0}}}{{16}}$$
Answer :
$$\frac{{{I_0}}}{8}$$
215. A lens having focal length $$f$$ and aperture of diameter $$d$$ forms an image of intensity $$I.$$ Aperture of diameter $$\frac{d}{2}$$ in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
A
$$f\,{\text{and}}\,\frac{I}{4}$$
B
$$\frac{{3f}}{4}\,{\text{and}}\,\frac{I}{2}$$
C
$$f\,{\text{and}}\,\frac{{3I}}{4}$$
D
$$\frac{f}{2}\,{\text{and}}\,\frac{I}{2}$$
Answer :
$$f\,{\text{and}}\,\frac{{3I}}{4}$$
216. An object is moving with speed $${v_0}$$ towards a spherical mirror with radius of curvature $$R,$$ along the central axis of the mirror. The speed of the image with respect to the mirror is ($$U$$ is the distance of the object from mirror at any given time $$t$$)
A
$$ + \left( {\frac{R}{{U - 2R}}} \right)v_0^2$$
B
$$ - {\left( {\frac{R}{{R - 2U}}} \right)^2}{v_0}$$
C
$$ - {\left( {\frac{R}{{2U - 2R}}} \right)^2}{v_0}$$
D
$$ + \left( {\frac{R}{{2U - 2}}} \right)v_0^2$$
Answer :
$$ - {\left( {\frac{R}{{R - 2U}}} \right)^2}{v_0}$$
217. A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is $$\frac{4}{3}$$ and the fish is $$12\,cm$$ below the surface, the radius of this circle (in $$cm$$ ) is -
A
$$36\sqrt 5 $$
B
$$4\sqrt 5 $$
C
$$36\sqrt 7 $$
D
$$\frac{{36}}{{\sqrt 7 }}$$
Answer :
$$\frac{{36}}{{\sqrt 7 }}$$
218.
Match the corresponding entries of Column 1 with Column 2. [Where $$m$$ is the magnification produced by the mirror]
Column 1
Column 2
1. $$m=-2$$
a. Convex mirror
2. $$m = - \frac{1}{2}$$
b. Concave mirror
3. $$m=+2$$
c. Real image
4. $$m = + \frac{1}{2}$$
d. Virtual image
A
1 → a and c; 2 → a and d; 3 → a and b; 4 → c and d
B
1 → a and d; 2 → b and c; 3 → b and d; 4 → 2 and c
C
1 → c and d; 2 → b and d; 3 → b and c; 4 → a and d
D
1 → b and c; 2 → b and c; 3 → b and d; 4 → a and d
Answer :
1 → b and c; 2 → b and c; 3 → b and d; 4 → a and d
219. A student measures the focal length of a convex lens by putting an object pin at a distance $$'u’$$ from the lens and measuring the distance $$'v’$$ of the image pin. The graph between $$'u’$$ and $$'v’$$ plotted by the student should look like
A


B


C


D


Answer :


220. Two thin lenses of focal lengths $${f_1}$$ and $${f_2}$$ are in contact and coaxial. The power of the combination is
A
$$\sqrt {\frac{{{f_1}}}{{{f_2}}}} $$
B
$$\sqrt {\frac{{{f_2}}}{{{f_1}}}} $$
C
$$\frac{{{f_1} + {f_2}}}{2}$$
D
$$\frac{{{f_1} + {f_2}}}{{{f_1}{f_2}}}$$
Answer :
$$\frac{{{f_1} + {f_2}}}{{{f_1}{f_2}}}$$


