161. Rainbows are formed by
A
reflection and diffraction
B
refraction and scattering
C
dispersion and total internal reflection
D
interference only
Answer :
dispersion and total internal reflection
162.
A plane mirror is kept parallel to $$y$$-axis. A point object is approaching the mirror with velocity $$\vec u = \left( {10\hat i + 10\hat j} \right)m/s.$$ The magnitude of relative velocity of objective w.r.t image is equal to

A
$$20\,\sqrt 2 \,m/s$$
B
$$20\,m/s$$
C
$$10\,\sqrt 2 \,m/s$$
D
$$10\,m/s$$
Answer :
$$20\,m/s$$
163.
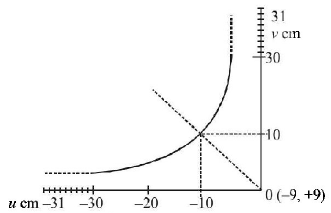
The graph shows relationship between object distance and image distance for a equiconvex lens. Then, focal length of the lens is

A
$$0.50 \pm 0.05\,cm$$
B
$$0.50 \pm 0.10\,cm$$
C
$$5.00 \pm 0.05\,cm$$
D
$$5.00 \pm 0.10\,cm$$
Answer :
$$5.00 \pm 0.05\,cm$$
164. The refractive index of the material of a prism is $$\sqrt 2 $$ and its refracting angle is $${30^ \circ }.$$ One of the refracting surfaces of the prism is made a mirror inwards. A beam of monochromatic light entering the prism from the other face will retrace its path after reflection from the mirrored surface, if its angle of incidence on the prism is
A
$${45^ \circ }$$
B
$${60^ \circ }$$
C
$${0^ \circ }$$
D
$${30^ \circ }$$
Answer :
$${45^ \circ }$$
165. A ray of light is incident at an angle of incidence, $$i,$$ on one face of a prism of angle $$A$$ (assumed to be small) and emerges normally from the opposite face. If the refractive index of the prism is $$\mu ,$$ the angle of incidence $$i,$$ is nearly equal to
A
$$\mu A$$
B
$$\frac{{\mu A}}{2}$$
C
$$\frac{A}{\mu }$$
D
$$\frac{A}{{2\mu }}$$
Answer :
$$\mu A$$
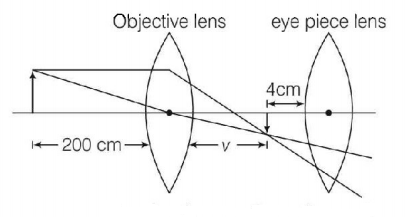
166. A astronomical telescope has objective and eyepiece of focal lengths $$40\,cm$$ $$4\,cm$$ respectively. To view an object $$200\,cm$$ away from the objective, the lenses must be separated by a distance
A
$$46.0\,cm$$
B
$$50.0\,cm$$
C
$$54.0\,cm$$
D
$$37.3\,cm$$
Answer :
$$54.0\,cm$$
167. Wavelength of light used in an optical instrument are $${\lambda _1} = 4000\,\mathop {\text{A}}\limits^ \circ \,\,{\text{and }}{\lambda _2} = 5000\,\mathop {\text{A}}\limits^ \circ ,$$ then ratio of their respective resolving powers (corresponding to $${\lambda _1}$$ and $${\lambda _2}$$ ) is
A
16 : 25
B
9 : 1
C
4 : 5
D
5 : 4
Answer :
5 : 4
168. The angle of a prism is $$A.$$ One of its refracting surfaces is silvered. Light rays falling at an angle of incidence $$2A$$ on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index $$\mu ,$$ of the prism is
A
$$2\sin A$$
B
$$2\cos A$$
C
$$\frac{1}{2}\cos A$$
D
$$\tan A$$
Answer :
$$2\cos A$$
169.
A ball is dropped from a height of $$20\,m$$ above the surface of water in a lake. The refractive index of water is $$4.3.$$ A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is $$12.8\,m$$ above the water surface, the fish sees the speed of ball as
[Take $$g = 10\,m/{s^2}.$$
A
$$9\,m/s$$
B
$$12\,m/s$$
C
$$16\,m/s$$
D
$$21.33\,m/s$$
Answer :
$$16\,m/s$$
170. The wavelength of light of frequency $$100\,Hz$$ is
A
$$2 \times {10^6}m$$
B
$$3 \times {10^6}m$$
C
$$4 \times {10^6}m$$
D
$$5 \times {10^6}m$$
Answer :
$$3 \times {10^6}m$$