151. Consider telecommunication through optical fibres. Which of the following statements is not true?
A
Optical fibres can be of graded refractive index
B
Optical fibres are subject to electromagnetic interference from outside
C
Optical fibres have extremely low transmission loss
D
Optical fibres may have homogeneous core with a suitable cladding.
Answer :
Optical fibres are subject to electromagnetic interference from outside
152.
In Fig. $$ABC$$ is the cross section of a right - angled prism and $$ACDE$$ is the cross section of a glass slab. The value of $$\theta $$ so that incident normally on the face $$AB$$ does not cross the face $$AC$$ is (given $${\sin ^{ - 1}}\left( {\frac{3}{5}} \right) = {37^ \circ }$$ ).
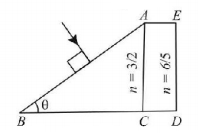
A
$$\theta \leqslant {37^ \circ }$$
B
$$\theta < {37^ \circ }$$
C
$$\theta \leqslant {53^ \circ }$$
D
$$\theta < {53^ \circ }$$
Answer :
$$\theta < {37^ \circ }$$
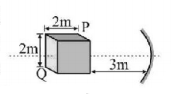
153.
A cube of side $$2\,m$$ is placed in front of a concave mirror of focal length $$1\,m$$ with its face $$P$$ at a distance of $$3\,m$$ and face $$Q$$ at a distance of $$5\,m$$ from the mirror. The distance between the image of face $$P$$ and $$Q$$ is
A
$$1\,m$$
B
$$1.5\,m$$
C
$$0.5\,m$$
D
$$0.25\,m$$
Answer :
$$0.25\,m$$
154. Two beams of red and violet colours are made to pass separately through a prism (angle of the prism is $${60^ \circ }$$ ). In the position of minimum deviation, the angle of refraction will be
A
$${30^ \circ }$$ for both the colours
B
greater for the violet colour
C
greater for the red colour
D
equal but not $${30^ \circ }$$ for both the colours
Answer :
$${30^ \circ }$$ for both the colours
155. A ray of light travelling in the direction $$\frac{1}{2}\left( {\hat i + \sqrt 3 \hat j} \right)$$ is incident on a plane mirror. After reflection, it travels along the direction $$\frac{1}{2}\left( {\hat i - \sqrt 3 \hat j} \right).$$ The angle of incidence is
A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${60^ \circ }$$
D
$${75^ \circ }$$
Answer :
$${30^ \circ }$$
156. An object $$2.4\,m$$ in front of a lens forms a sharp image on a film $$12\,cm$$ behind the lens. A glass plate $$1\,cm$$ thick, of refractive index 1.50 is interposed between lens and film with its plane faces parallel to film. At what distance (from lens) should object shifted to be in sharp focus of film?
A
$$7.2\,m$$
B
$$2.4\,m$$
C
$$3.2\,m$$
D
$$5.6\,m$$
Answer :
$$5.6\,m$$
157. The focal length of the objective and the eyepiece of a telescope are $$50\,cm$$ and $$5\,cm$$ respectively. If the telescope is focused for distinct vision on a scale distant $$2\,m$$ from its objective, then its magnifying power will be :
A
$$- 4$$
B
$$- 8$$
C
$$+ 8$$
D
$$- 2$$
Answer :
$$- 2$$
158. A ray is incident at an angle of incidence $$i$$ on one surface of a prism of small angle $$A$$ and emerge normally from opposite surface. If the refractive index of the material of prism is $$\mu ,$$ the angle of incidence $$i$$ is nearly equal to
A
$$\frac{A}{\mu }$$
B
$$\frac{A}{{2\mu }}$$
C
$$\mu A$$
D
$$\frac{{\mu A}}{2}$$
Answer :
$$\mu A$$
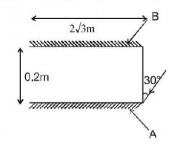
159.
Two plane mirrors $$A$$ and $$B$$ are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle $${30^ \circ }$$ at a point just inside one end of $$A.$$ The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (including the first one) before it emerges out is
A
28
B
30
C
32
D
34
Answer :
30
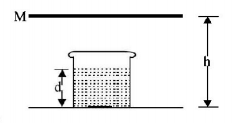
160.
A plane mirror is held at a height $$h$$ above the bottom of an empty beaker. The beaker is now filled with water up to depth $$d.$$ The general expression for the distance from a scratch at the bottom of the beaker to its image in terms of $$h$$ and the depth $$d$$ of water in the beaker is
A
$$2h - d\left( {\frac{\mu }{{\mu - 1}}} \right)$$
B
$$2h - \frac{d}{2}\left( {\frac{{\mu - 1}}{\mu }} \right)$$
C
$$2h - d\left( {\frac{{\mu - 1}}{\mu }} \right)$$
D
$$2h - d\left( {\frac{{2\mu - 1}}{\mu }} \right)$$
Answer :
$$2h - d\left( {\frac{{\mu - 1}}{\mu }} \right)$$