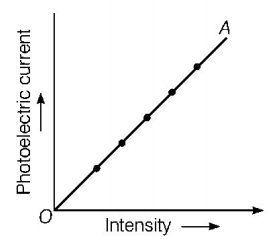
71. Which of the following figures represent the variation of particle momentum and the associated de-Broglie wavelength?
A
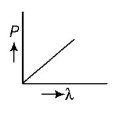

B
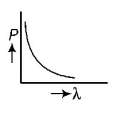

C


D


Answer :


72. Radiation of wavelength $$\lambda ,$$ is incident on a photocell. The fastest emitted electron has speed $$v.$$ If the wavelength is changed to $$\frac{{3\lambda }}{4},$$ the speed of the fastest emitted electron will be :
A
$$ = v{\left( {\frac{4}{3}} \right)^{\frac{1}{2}}}$$
B
$$ = v{\left( {\frac{3}{4}} \right)^{\frac{1}{2}}}$$
C
$$ > v{\left( {\frac{4}{3}} \right)^{\frac{1}{2}}}$$
D
$$ < v{\left( {\frac{4}{3}} \right)^{\frac{1}{2}}}$$
Answer :
$$ > v{\left( {\frac{4}{3}} \right)^{\frac{1}{2}}}$$
73. A radiation of energy $$E$$ falls normally on a perfectly reflecting surface. The momentum transferred to the surface is
A
$$Ec$$
B
$$\frac{{2E}}{c}$$
C
$$\frac{E}{c}$$
D
$$\frac{E}{{{c^2}}}$$
Answer :
$$\frac{{2E}}{c}$$
74. When ultraviolet rays are incident on metal plate, the photoelectric effect does not occur. It occurs by incidence of
A
infrared rays
B
X-rays
C
radiowaves
D
light waves
Answer :
X-rays
75. A light source is at a distance $$d$$ from a photoelectric cell, then the number of photoelectrons emitted from the cell is $$n.$$ If the distance of light source and cell is reduced to half, then the number of photoelectrons emitted will become
A
$$\frac{n}{2}$$
B
$$2\,n$$
C
$$4\,n$$
D
$$n$$
Answer :
$$4\,n$$
76. The maximum kinetic energy of the electrons hitting a target so as to produce X-ray of wavelength $$1\,\mathop {\text{A}}\limits^ \circ $$ is
A
$$1.24\,keV$$
B
$$12.4\,keV$$
C
$$124\,keV$$
D
None of these
Answer :
$$12.4\,keV$$
77. Light of wavelength $$200\,\mathop {\text{A}}\limits^ \circ $$ fall on aluminium surface. Work function of aluminium is $$4.2\,eV.$$ What is the kinetic energy of the fastest emitted photoelectrons?
A
$$2\,eV$$
B
$$1\,eV$$
C
$$4\,eV$$
D
$$0.2\,eV$$
Answer :
$$2\,eV$$
78. A photocell employs photoelectric effect to convert
A
change in the frequency of light into a change in electric voltage
B
change in the intensity of illumination into a change in photoelectric current
C
change in the intensity of illumination into a change in the work function of the photocathode
D
change in the frequency of light into a change in the electric current
Answer :
change in the intensity of illumination into a change in photoelectric current
79. The work function of a surface of a photosensitive material is $$6.2\,eV.$$ The wavelength of the incident radiation for which the stopping potential is $$5\,V$$ lies in the
A
ultraviolet region
B
visible region
C
infrared region
D
X-ray region
Answer :
X-ray region
80. Photons with energy $$5\,eV$$ are incident on a cathode $$C$$ in a photoelectric cell. The maximum energy of emitted photoelectrons is $$2\,eV.$$ When photons of energy $$6\,eV$$ are incident on $$C,$$ no photoelectrons will reach the anode $$A,$$ if the stopping potential of $$A$$ relative to $$C$$ is
A
$$+3\,V$$
B
$$+4\,V$$
C
$$-1\,V$$
D
$$-3\,V$$
Answer :
$$-3\,V$$