81.
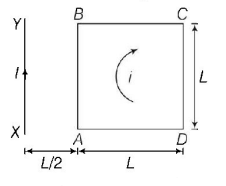
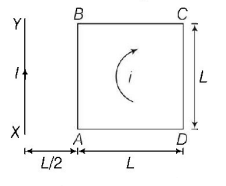
A square loop $$ABCD$$ carrying a current $$i,$$ is placed near and coplanar with a long straight conductor $$XY$$ carrying a current $$I,$$ the net force on the loop will be
A
$$\frac{{{\mu _0}li}}{{2\pi }}$$
B
$$\frac{{2{\mu _0}liL}}{{3\pi }}$$
C
$$\frac{{{\mu _0}liL}}{{2\pi }}$$
D
$$\frac{{2{\mu _0}li}}{{3\pi }}$$
Answer :
$$\frac{{2{\mu _0}li}}{{3\pi }}$$
82. A long solenoid has 500 turns. When a current of $$2\,A$$ is passed through it, the resulting magnetic flux linked with each turn of the solenoid is $$4 \times {10^{ - 3}}\,Wb.$$ The self-inductance of the solenoid is
A
$$2.5\,H$$
B
$$2\,H$$
C
$$1\,H$$
D
$$4\,H$$
Answer :
$$1\,H$$
83. When the current in a certain inductor coil is $$5.0\,A$$ and is increasing at the rate of $$10.0\,A/s,$$ the potential difference across the coil is $$140V.$$ When the current is $$5.0\,A$$ and decreasing at the rate of $$10.0\,A/s,$$ the potential difference is $$60V.$$ The self inductance of the coil is -
A
$$2\,H$$
B
$$4\,H$$
C
$$8\,H$$
D
$$12\,H$$
Answer :
$$4\,H$$
84. An ideal coil of $$10H$$ is connected in series with a resistance of $$5\Omega $$ and a battery of $$5V.$$ 2 second after the connection is made, the current flowing in ampere in the circuit is
A
$$\left( {1 - {e^{ - 1}}} \right)$$
B
$$\left( {1 - e} \right)$$
C
$$e$$
D
$${e^{ - 1}}$$
Answer :
$$\left( {1 - {e^{ - 1}}} \right)$$
85. The magnetic field in a region is given by $$B = {B_0}\left( {1 + \frac{x}{a}} \right)\hat k.$$ A square loop of edge-length $$d$$ is placed with its edges along the $$x$$ and $$y$$ -axes. The loop is moved with a constant velocity $$v = {v_0}\hat i.$$ The emf induced in the loop is :
A
zero
B
$${v_0}{B_0}d$$
C
$$\frac{{{v_0}{B_0}{d^3}}}{{{a^2}}}$$
D
$$\frac{{{v_0}{B_0}{d^2}}}{a}$$
Answer :
$$\frac{{{v_0}{B_0}{d^2}}}{a}$$
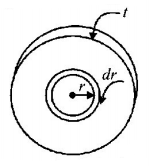
86. A conducting disc of conductivity $$\sigma $$ has a radius $$'a'$$ and thickness $$'t'.$$ If the magnetic field $$B$$ is applied in a direction perpendicular to the plane of the disc changes with time at the rate of $$\frac{{dB}}{{dt}} = \alpha .$$ Calculate the power dissipated in the disc due to the induced current.
A
$$\frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
B
$$\frac{{\pi t\sigma {a^4}}}{4}{\alpha ^2}$$
C
$$\frac{{\pi t\sigma {a^4}}}{2}{\alpha ^2}$$
D
$$\frac{{2\pi t\sigma {a^4}}}{3}{\alpha ^2}$$
Answer :
$$\frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
87.
$$ABCD$$ is a wire frame in the shape of an isosceles trapezium (i.e., length $$AB =$$ length $$CD$$ ) enter a magnetic field with flux density $$B$$ at $$t = 0$$ as shown in the figure. If the total resistance of wire frame is $$R.$$ What is the value of the induced current in the wire frame after $$t$$ seconds, assuming that the frame has to entered the field completely by then?
[$$v$$ = Velocity of frame]
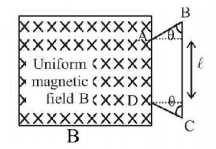
A
zero
B
$$\frac{{Bv}}{R}\left( {2\,vt\sin \theta + \ell } \right)$$
C
$$\frac{{Bv}}{R}\left( {\frac{{2\,vt}}{{\tan \theta }} + \ell } \right)$$
D
$$\frac{B}{v}$$
Answer :
$$\frac{{Bv}}{R}\left( {\frac{{2\,vt}}{{\tan \theta }} + \ell } \right)$$
88.
An electric potential difference will be induced between the ends of the conductor as shown in the diagram, when the conductor moves in the direction
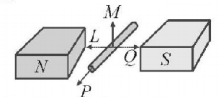
A
$$P$$
B
$$Q$$
C
$$L$$
D
$$M$$
Answer :
$$M$$
89.
A rectangular coil has a long straight wire passing through its centroid perpendicular to its plane as shown. If current through the wire varies as $$i = {i_0}\sin \omega t,$$ induced current in the coil will be (Given $$R$$ = Resistance of the coil)
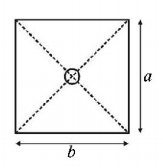
A
$$\frac{{{i_0}\sin \omega t}}{R}$$
B
$$\frac{{\pi a\sin \omega t}}{{bR}}$$
C
zero
D
$$\frac{{\pi a\cos \omega t}}{{bR}}$$
Answer :
zero
90. In an $$AC$$ generator, a coil with $$N$$ turns, all of the same area $$A$$ and total resistance $$R,$$ rotates with frequency $$\omega $$ in a magnetic field $$B.$$ The maximum value of emf generated in the coil is
A
N.A.B.R.$$\omega $$
B
N.A.B
C
N.A.B.R
D
N.A.B.$$\omega $$
Answer :
N.A.B.$$\omega $$