151.
An equilateral triangular loop having a resistance $$R$$ and length of each side $$\ell $$ is placed in a magnetic field which is varying at $$\frac{{dB}}{{dt}} = 1\,T/s.$$ The induced current in the loop will be

A
$$\frac{{\sqrt 3 }}{4}\frac{{{\ell ^2}}}{R}$$
B
$$\frac{4}{{\sqrt 3 }}\frac{{{\ell ^2}}}{R}$$
C
$$\frac{{\sqrt 3 }}{4}\frac{R}{{{\ell ^2}}}$$
D
$$\frac{4}{{\sqrt 3 }}\frac{R}{{{\ell ^2}}}$$
Answer :
$$\frac{{\sqrt 3 }}{4}\frac{{{\ell ^2}}}{R}$$
152.
$$PQ$$ is an infinite current carrying conductor. $$AB$$ and $$CD$$ are smooth conducting rods on which a conductor $$EF$$ moves with constant velocity $$v$$ as shown. The force needed to maintain constant speed of $$EF$$ is
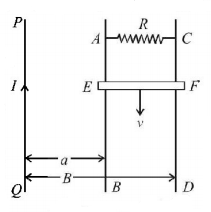
A
$$\frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
B
$${\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{a}{b}} \right)} \right]^2}\frac{1}{{vR}}$$
C
$${\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}\frac{v}{R}$$
D
$$\frac{v}{R}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{a}{b}} \right)} \right]^2}$$
Answer :
$$\frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
153.
In the circuit of figure, the bulb will become suddenly bright, if

A
contact is made or broken
B
contact is made
C
contact is broken
D
None of the above
Answer :
contact is broken
154. In a conducting cycle wheel (of $$n$$ spokes), each spoke of length $$\ell $$ is rotating with angular speed $$\omega $$ in uniform perpendicular magnetic field $$B.$$ If due to flux cutting each metal spoke behaves as an identical cell of emf $$\left( e \right)$$ then net emf of the system is
A
$$nB\omega {l^2}$$
B
$$\frac{1}{2}nB\omega {l^2}$$
C
$$\frac{1}{2}B\omega {l^2}$$
D
$$B\omega {l^2}$$
Answer :
$$\frac{1}{2}B\omega {l^2}$$
155. Two coils are placed close to each other. The mutual inductance of the pair of coils depends upon
A
the rates at which currents are changing in the two coils
B
relative position and orientation of the two coils
C
the materials of the wires of the coils
D
the currents in the two coils
Answer :
relative position and orientation of the two coils
156. In a region of uniform magnetic induction $$B = {10^{ - 2}}T,$$ a circular coil of radius $$30\,cm$$ and resistance $${\pi ^2}\,ohm$$ is rotated about an axis which is perpendicular to the direction of $$B$$ and which forms a diameter of the coil. If the coil rotates at $$200\,rpm$$ the amplitude of the alternating current induced in the coil is
A
$$4\,{\pi ^2}mA$$
B
$$30\,mA$$
C
$$6\,mA$$
D
$$200\,mA$$
Answer :
$$6\,mA$$
157.
A conducting rod of mass $$m$$ and $$\ell $$ is placed on a smooth horizontal surface in a region where transverse uniform magnetic field $$B$$ exists in the region. At $$t = 0,$$ constant force $$F$$ starts acting on the rod at its mid point as shown. Potential difference between ends of the rod, $${V_P} - {V_Q}$$ at any time $$t$$ is

A
$$\frac{{BF\ell t}}{{2m}}$$
B
$$\frac{{BF\ell t}}{{4m}}$$
C
$$\frac{{5BF\ell t}}{{8m}}$$
D
$$\frac{{7BF\ell t}}{{8m}}$$
Answer :
$$\frac{{BF\ell t}}{{2m}}$$
158. Two identical circular loops of metal wire are lying on a table without touching each other. Loop-$$A$$ carries a current which increases with time. In response, the loop-$$B$$
A
remains stationary
B
is attracted by the loop-$$A$$
C
is repelled by the loop-$$A$$
D
rotates about its $$CM,$$ with $$CM$$ fixed
Answer :
is repelled by the loop-$$A$$
