111. When the current changes from $$+2\,A$$ to $$-2\,A$$ in 0.05 second, an e.m.f. of $$8 V$$ is induced in a coil. The coefficient of self-induction of the coil is
A
$$0.2\,H$$
B
$$0.4\,H$$
C
$$0.8\,H$$
D
$$0.1\,H$$
Answer :
$$0.1\,H$$
112. The total number of turns and cross-section area in a solenoid is fixed. However, its length $$L$$ is varied by adjusting the separation between windings. The inductance of solenoid will be proportional to:
A
$$L$$
B
$${L^2}$$
C
$$\frac{1}{{{L^2}}}$$
D
$$\frac{1}{L}$$
Answer :
$$\frac{1}{L}$$
113.
The flux linked with a coil at any instant $$'t'$$ is given by
$$\phi = 10{t^2} - 50t + 250$$
The induced emf at $$t = 3s$$ is
A
$$-190\,V$$
B
$$-10\,V$$
C
$$10\,V$$
D
$$190\,V$$
Answer :
$$-10\,V$$
114. A thin circular ring of area $$A$$ is held perpendicular to a uniform magnetic field of induction $$B.$$ $$A$$ small cut is made in the ring and a galvanometer is connected across the ends such that the total resistance of the circuit is $$R.$$ When the ring is suddenly squeezed to zero area, the charge flowing through the galvanometer is
A
$$\frac{{BR}}{A}$$
B
$$\frac{{AB}}{R}$$
C
$$ABR$$
D
$$\frac{{{B^2}A}}{{{R^2}}}$$
Answer :
$$\frac{{AB}}{R}$$
115. An EM wave from air enters a medium. The electric fields are $$\overrightarrow {{E_1}} = {E_{01}}\hat x\cos \left[ {2\pi v\left( {\frac{z}{c} - t} \right)} \right]$$ in air and $$\overrightarrow {{E_2}} = {E_{02}}\hat x\cos \left[ {k\left( {2z - ct} \right)} \right]$$ in medium, where the wave number $$k$$ and frequency $$v$$ refer to their values in air. The medium is nonmagnetic. If $${ \in _{{r_1}}}$$ and $${ \in _{{r_2}}}$$ refer to relative permittivities of air and medium respectively, which of the following options is correct?
A
$$\frac{{{ \in _{{r_1}}}}}{{{ \in _{{r_2}}}}} = 4$$
B
$$\frac{{{ \in _{{r_1}}}}}{{{ \in _{{r_2}}}}} = 2$$
C
$$\frac{{{ \in _{{r_1}}}}}{{{ \in _{{r_2}}}}} = \frac{1}{4}$$
D
$$\frac{{{ \in _{{r_1}}}}}{{{ \in _{{r_2}}}}} = \frac{1}{2}$$
Answer :
$$\frac{{{ \in _{{r_1}}}}}{{{ \in _{{r_2}}}}} = \frac{1}{4}$$
116.
Two coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area $$A = 10\,c{m^2}$$ and length = $$20\,cm.$$ If one of the solenoid has 300 turns and the other 400 turns, their mutual inductance is
$$\left( {{\mu _0} = 4\mu \times {{10}^{ - 7}}Tm{A^{ - 1}}} \right)$$
A
$$2.4\pi \times {10^{ - 5}}H$$
B
$$4.8\pi \times {10^{ - 4}}H$$
C
$$4.8\pi \times {10^{ - 5}}H$$
D
$$2.4\pi \times {10^{ - 4}}H$$
Answer :
$$2.4\pi \times {10^{ - 4}}H$$
117. What is the self-inductance of a coil which produces $$5\,V$$ when the current changes from $$3\,A$$ to $$2\,A$$ in one millisecond ?
A
$$5000\,H$$
B
$$5\,mH$$
C
$$50\,H$$
D
$$5\,H$$
Answer :
$$5\,mH$$
118. A coil of inductance $$8.4 mH$$ and resistance $$6\,\Omega $$ is connected to a $$12 V$$ battery. The current in the coil is $$1.0 A$$ at approximately the time
A
$$500 s$$
B
$$25 s$$
C
$$35 ms$$
D
$$1 ms$$
Answer :
$$1 ms$$
119. A short-circuited coil is placed in a time-varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the wire radius halved, the electrical power dissipated would be
A
halved
B
the same
C
doubled
D
quadrupled
Answer :
the same
120.
A thin semicircular conducting ring $$\left( {PQR} \right)$$ of radius $$r$$ is falling with its plane vertical in a horizontal magnetic field $$B,$$ as shown in figure. The potential difference developed across the ring when its speed is $$v,$$ is
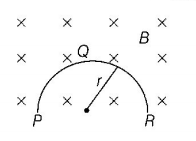
A
zero
B
$$\frac{{BV\pi {r^2}}}{2}$$ and $$P$$ is at higher potential
C
$$\pi rBv$$ and $$R$$ is at higher potential
D
$$2rBv$$ and $$R$$ is at higher potential
Answer :
$$2rBv$$ and $$R$$ is at higher potential