121.
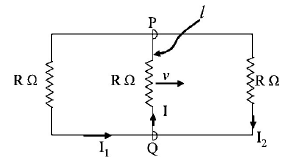
A rectangular loop has a sliding connector $$PQ$$ of length $$l$$ and resistance $$R\,\Omega $$ and it is moving with a speed $$v$$ as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents $${I_1},{I_2}$$ and $$I$$ are
A
$${I_1} = - {I_2} = \frac{{Blv}}{{6R}},I = \frac{{2Blv}}{{6R}}$$
B
$${I_1} = {I_2} = \frac{{Blv}}{{3R}},I = \frac{{2Blv}}{{3R}}$$
C
$${I_1} = {I_2} = I = \frac{{Blv}}{R}$$
D
$${I_1} = {I_2} = \frac{{Blv}}{{6R}},I = \frac{{Blv}}{{3R}}$$
Answer :
$${I_1} = {I_2} = \frac{{Blv}}{{3R}},I = \frac{{2Blv}}{{3R}}$$
122.
An inductor $$\left( {L = 0.03H} \right)$$ and a resistor $$\left( {R = 0.15\Omega } \right)$$ are connected in series to a battery of $$15V$$ EMF in a circuit shown below. The key $${K_1}$$ has been kept closed for a long time. Then at $$t = 0,$$ $${K_1}$$ is opened and key $${K_2}$$ is closed simultaneously. At $$t = 1 ms,$$ the current in the circuit will be : $$\left( {{e^5} \cong 150} \right)$$

A
$$6.7\,mA$$
B
$$0.67\,mA$$
C
$$100\,mA$$
D
$$67\,mA$$
Answer :
$$0.67\,mA$$
123. A horizontal straight wire $$20\,m$$ long extending from east to west falling with a speed of $$5.0\,m/s,$$ at right angles to the horizontal component of the earth’s magnetic field $$0.30 \times {10^{ - 4}}\,Wb/{m^2}.$$ The instantaneous value of the e.m.f. induced in the wire will be
A
$$3\,mV$$
B
$$4.5\,mV$$
C
$$1.5\,mV$$
D
$$6.0\,mV$$
Answer :
$$3\,mV$$
124.
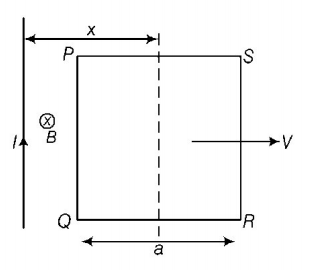
A conducting square frame of side $$'a'$$ and a long straight wire carrying current $$I$$ are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity $$'v'.$$ The emf induced in the frame will be proportional to

A
$$\frac{1}{{{x^2}}}$$
B
$$\frac{1}{{{{\left( {2x - a} \right)}^2}}}$$
C
$$\frac{1}{{{{\left( {2x + a} \right)}^2}}}$$
D
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
Answer :
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
125.
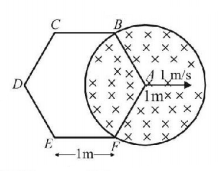
A cylindrical region of radius $$1\,m$$ has instantaneous homogenous magnetic field of $$5T$$ and it is increasing at a rate of $$2T/s.$$ A regular hexagonal loop $$ABCDEFA$$ of side $$1\,m$$ is being drawn in to the region with a constant speed of $$1\,m/s$$ as shown in the figure. What is the magnitude of emf developed in the loop just after the shown instant when the corner $$A$$ of the hexagon is coinciding with the centre of the circle ?
A
$$\frac{5}{{\sqrt 3 }}V$$
B
$$\frac{{2\pi }}{3}V$$
C
$$\left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V$$
D
$$\left( {5\sqrt 3 + \pi } \right)V$$
Answer :
$$\left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V$$
126. A small square loop of wire of side $$\ell $$ is placed inside a large square loop of wire of side $$L\left( {L > \ell } \right).$$ The loop are coplanar and their centre coincide. The mutual inductance of the system is proportional to
A
$$\frac{\ell }{L}$$
B
$$\frac{{{\ell ^2}}}{L}$$
C
$$\frac{L}{\ell }$$
D
$$\frac{{{L^2}}}{\ell }$$
Answer :
$$\frac{{{\ell ^2}}}{L}$$
127. A thin circular ring of area $$A$$ is perpendicular to uniform magnetic field of induction $$B.$$ A small cut is made in the ring and a galvanometer is connected across the ends such that the total resistance of circuit is $$R.$$ When the ring is suddenly squeezed to zero area, the charge flowing through the galvanometer is
A
$$\frac{{BR}}{A}$$
B
$$\frac{{AB}}{R}$$
C
$$ABR$$
D
$$\frac{{{B^2}A}}{{{R^2}}}$$
Answer :
$$\frac{{AB}}{R}$$
128. The back e.m.f. in a $$d.c.$$ motor is maximum, when
A
the motor has picked up max speed
B
the motor has just started moving
C
the speed of motor is still on the increase
D
the motor has just been switched off
Answer :
the motor has picked up max speed
129.
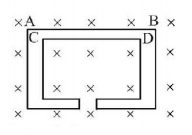
A wire is bent to form the double loop shown in Fig. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing, the current will flow from
A
$$a$$ to $$b$$ and $$c$$ to $$d$$
B
$$b$$ to $$a$$ and $$d$$ to $$c$$
C
$$a$$ to $$b$$ and $$d$$ to $$c$$
D
$$b$$ to $$a$$ and $$c$$ to $$d$$
Answer :
$$a$$ to $$b$$ and $$d$$ to $$c$$
130. Two coils, one primary of $$500$$ turns and one secondary of $$25$$ turns, are wound on an iron ring of mean diameter $$20\,cm$$ and cross-sectional area $$12\,c{m^2}.$$ If the permeability of iron is $$800,$$ the mutual inductance is :
A
$$0.48\,H$$
B
$$2.4\,H$$
C
$$0.12\,H$$
D
$$0.24\,H$$
Answer :
$$0.24\,H$$