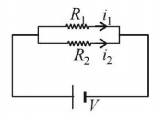
251. Two cities are $$150\,km$$ apart. Electric power is sent from one city to another city through copper wires. The fall of potential per $$km$$ is $$8$$ volt and the average resistance per $$km$$ is $$0.5\,\Omega .$$ The power loss in the wires is :
A
$$19.2\,W$$
B
$$19.2\,kW$$
C
$$19.2\,J$$
D
$$12.2\,kW$$
Answer :
$$19.2\,kW$$
252. An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii arein the ratio of $$\frac{4}{3}$$ and $$\frac{2}{3},$$ then the ratio of the current passing through the wires will be
A
$$\frac{8}{9}$$
B
$$\frac{1}{3}$$
C
$$3$$
D
$$2$$
Answer :
$$\frac{1}{3}$$
253.
The total power dissipated in watts in the circuit shown here is
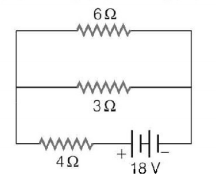
A
16
B
40
C
54
D
4
Answer :
54
254. The resistance of hot tungsten filament is about 10 times the cold resistance. What will be the resistance of $$100\,W$$ and $$200\,V$$ lamp when not in use ?
A
$$20\Omega $$
B
$$40\Omega $$
C
$$200\Omega $$
D
$$400\Omega $$
Answer :
$$40\Omega $$
255. If the resistance of a conductor is $$5\Omega $$ at $${50^ \circ }C\,\& \,7\Omega $$ at $${100^ \circ }C,$$ then mean temperature coefficient of resistance (of material) is
A
$$0.013{/^ \circ }C$$
B
$$0.004{/^ \circ }C$$
C
$$0.006{/^ \circ }C$$
D
$$0.008{/^ \circ }C$$
Answer :
$$0.013{/^ \circ }C$$
256.
The diagrams below show regions of equipotentials.
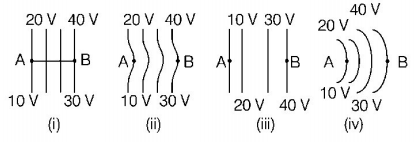
A positive charge is moved from $$A$$ to $$B$$ in each diagram.
A
Maximum work is required to move $$q$$ in figure (iii)
B
In all the four cases, the work done is the same
C
Minimum work is required to move $$q$$ in figure (i)
D
Maximum work is required to move $$q$$ in figure (ii)
Answer :
In all the four cases, the work done is the same
257. If a wire of resistance $$R$$ is melted and recasted to half of its length, then the new resistance of the wire will be
A
$$\frac{R}{4}$$
B
$$\frac{R}{2}$$
C
$$R$$
D
$$2R$$
Answer :
$$\frac{R}{4}$$
258. A galvanometer has a coil of resistance $$100\,\Omega $$ and gives a full scale deflection for $$30\,mA$$ current. If it is to work as a voltmeter of $$30\,V$$ range, the resistance required to be added will be
A
$$900\,\Omega $$
B
$$1800\,\Omega $$
C
$$500\,\Omega $$
D
$$1000\,\Omega $$
Answer :
$$900\,\Omega $$
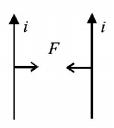
259. Two thin, long, parallel wires, separated by a distance $$'d'$$ carry a current of $$'i'$$ $$A$$ in the same direction. They will
A
repel each other with a force of $$\frac{{{\mu _0}{i^2}}}{{\left( {2\pi d} \right)}}$$
B
attract each other with a force of $$\frac{{{\mu _0}{i^2}}}{{\left( {2\pi d} \right)}}$$
C
repel each other with a force of $$\frac{{{\mu _0}{i^2}}}{{\left( {2\pi {d^2}} \right)}}$$
D
attract each other with a force of $$\frac{{{\mu _0}{i^2}}}{{\left( {2\pi {d^2}} \right)}}$$
Answer :
attract each other with a force of $$\frac{{{\mu _0}{i^2}}}{{\left( {2\pi d} \right)}}$$
260. If a neglegibly small current is passed through a wire of length $$15\,m$$ and of resistance $$5\,\Omega $$ having uniform cross-section of $$6 \times {10^{ - 7}}{m^2},$$ then coefficient of resistivity of material, is
A
$$1 \times {10^{ - 7}}\Omega - m$$
B
$$2 \times {10^{ - 7}}\Omega - m$$
C
$$3 \times {10^{ - 7}}\Omega - m$$
D
$$4 \times {10^{ - 7}}\Omega - m$$
Answer :
$$2 \times {10^{ - 7}}\Omega - m$$