201.
Find the equivalent resistance between $$A$$ and $$E$$ (resistance of each resistor is $$R.$$)

A
$$\frac{7}{{12}}R$$
B
$$\frac{7}{{13}}R$$
C
$$\frac{7}{{15}}R$$
D
$$\frac{8}{{13}}R$$
Answer :
$$\frac{7}{{12}}R$$
202. The velocity of charge carriers of current (about $$1A$$ ) in a metal under normal conditions is of the order of
A
a fraction of $$mm/s$$
B
velocity of light
C
several thousand $$m/s$$
D
a few hundred $$m/s$$
Answer :
a fraction of $$mm/s$$
203. The specific resistance of a conductor increases with
A
increase in temperature
B
increase in cross-sectional area
C
decrease in length
D
decrease in cross-sectional area
Answer :
increase in temperature
204.
When the switch $$S,$$ in the circuit shown, is closed then the valued of current $$i$$ will be :

A
$$3A$$
B
$$5A$$
C
$$4A$$
D
$$2A$$
Answer :
$$5A$$
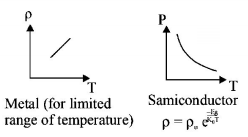
205. The temperature dependence of resistances of $$Cu$$ and undoped $$Si$$ in the temperature range $$300 - 400\,K,$$ is best described by :
A
Linear increase for $$Cu,$$ exponential decrease of $$Si.$$
B
Linear decrease for $$Cu,$$ linear decrease for $$Si.$$
C
Linear increase for $$Cu,$$ linear increase for $$Si.$$
D
Linear increase for $$Cu,$$ exponential increase for $$Si.$$
Answer :
Linear increase for $$Cu,$$ exponential decrease of $$Si.$$
206. A material $$'B'$$ has twice the specific resistance of $$'A'.$$ A circular wire made of $$'B'$$ has twice the diameter of a wire made of $$'A'$$ then for the two wires to have the same resistance, the ratio $$\frac{{{l_B}}}{{{l_A}}}$$ of their respective lengths must be
A
1
B
$$\frac{1}{2}$$
C
$$\frac{1}{4}$$
D
$$2$$
Answer :
$$2$$
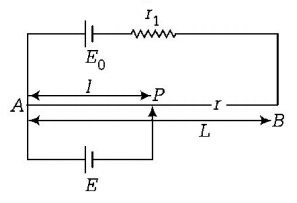
207. A potentiometer wire of length $$L$$ and a resistance $$r$$ are connected in series with a battery of e.m.f. $${E_0}$$ and a resistance $${r_1}.$$ An unknown e.m.f. is balanced at a length $$l$$ of the potentiometer wire. The e.m.f. $$E$$ will be given by
A
$$\frac{{L{E_0}r}}{{l{r_1}}}$$
B
$$\frac{{{E_0}r}}{{\left( {r + {r_1}} \right)}} \cdot \frac{l}{L}$$
C
$$\frac{{{E_0}l}}{L}$$
D
$$\frac{{L{E_0}r}}{{\left( {r + {r_1}} \right)l}}$$
Answer :
$$\frac{{{E_0}r}}{{\left( {r + {r_1}} \right)}} \cdot \frac{l}{L}$$
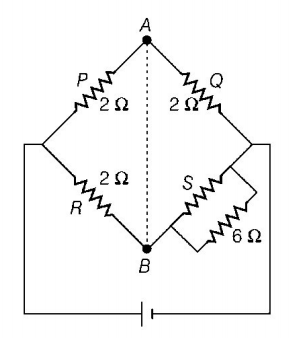
208. Three resistance $$P,Q,R$$ each of $$2\,\Omega $$ and an unknown resistance $$S$$ form the four arms of a Wheatstone bridge circuit. When a resistance of $$6\,\Omega $$ is connected in parallel to $$S$$ the bridge gets balanced. What is the value of $$S$$?
A
$$2\,\Omega $$
B
$$3\,\Omega $$
C
$$6\,\Omega $$
D
$$1\,\Omega $$
Answer :
$$3\,\Omega $$
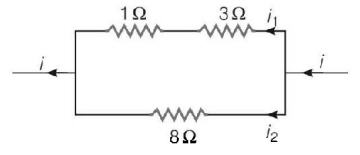
209.
Power dissipated across the $$8\,\Omega $$ resistor in the circuit shown here is $$2\,W.$$ The power dissipated in watt units across the $$3\,\Omega $$ resistor is

A
2.0
B
1.0
C
0.5
D
3.0
Answer :
3.0
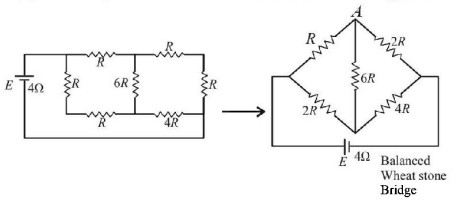
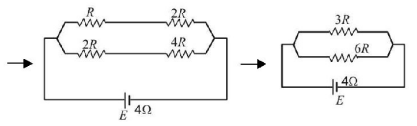
210.
A battery of internal resistance $$4\Omega $$ is connected to the network of resistances as shown. In order that the maximum power can be delivered to the network, the value of $$R$$ in $$\Omega $$ should be

A
$$\frac{4}{9}$$
B
2
C
$$\frac{8}{3}$$
D
18
Answer :
2