241. Two bulbs $$25\,W,220\,V$$ and $$100\,W,220\,V$$ are given. Which has higher resistance?
A
$$25\,W$$ bulb
B
$$100\,W$$ bulb
C
Both bulbs will have equal resistance
D
Resistance of bulbs cannot be compared
Answer :
$$25\,W$$ bulb
242.
Six identical resistors are connected as shown in the figure. The equivalent resistance will be
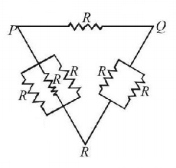
A
maximum between $$P$$ and $$R$$
B
maximum between $$Q$$ and $$R$$
C
maximum between $$P$$ and $$Q$$
D
All are equal
Answer :
maximum between $$P$$ and $$Q$$
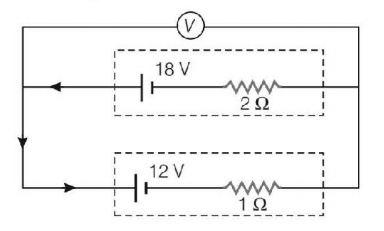
243.
Two batteries, one of emf $$18\,V$$ and internal resistance $$2\,\Omega $$ and the other of emf $$12\,V$$ and internal resistance $$1\,\Omega ,$$ are connected as shown. The voltmeter $$V$$ will record a reading of
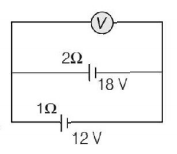
A
$$15\,V$$
B
$$30\,V$$
C
$$14\,V$$
D
$$18\,V$$
Answer :
$$14\,V$$
244. The resistance of a wire is $$R$$ ohm. If it is melted and stretched to $$n$$ times its original length, its new resistance will be
A
$$nR$$
B
$$\frac{R}{n}$$
C
$${n^2}R$$
D
$$\frac{R}{{{n^2}}}$$
Answer :
$${n^2}R$$
245. A $${5^ \circ }C$$ rise in temperature is observed in a conductor by passing a current. When the current is doubled the rise in temperature will be approximately
A
$${16^ \circ }C$$
B
$${10^ \circ }C$$
C
$${20^ \circ }C$$
D
$${12^ \circ }C$$
Answer :
$${20^ \circ }C$$
246. The internal resistance of a $$2.1\,V$$ cell which gives a current of $$0.2\,A$$ through a resistance of $$10\,\Omega $$ is
A
$$0.5\,\Omega $$
B
$$0.8\,\Omega $$
C
$$1.0\,\Omega $$
D
$$0.2\,\Omega $$
Answer :
$$0.5\,\Omega $$
247.
Consider the following two statements:
I. Kirchhoff’s junction law follows from the conservation of charge.
II. Kirchhoff’s loop law follows from the conservation of energy.
Which of the following is correct?
A
Both I and II are wrong
B
I is correct and II is wrong
C
I is wrong and II is correct
D
Both I and II are correct
Answer :
Both I and II are correct
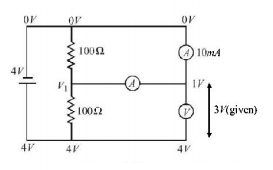
248.
In the figure ammeter $${A_1}$$ reads a current of $$10\,mA,$$ while the voltmeter reads a potential difference of $$3V.$$ What does ammeter $${A_2}$$ in $$mA$$ read ? The ammeters are identical, the internal resistance of the battery is negligible.
(Consider all ammeters and voltmeters as non-ideal.)
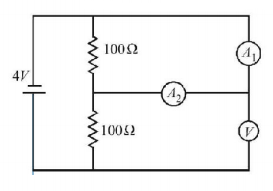
A
$$6.67\,mA$$
B
$$3.12\,mA$$
C
$$1.12\,mA$$
D
$$5.14\,mA$$
Answer :
$$6.67\,mA$$
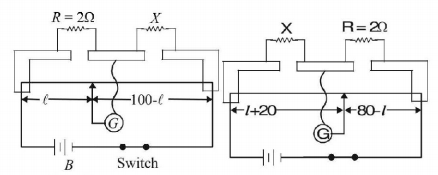
249. A resistance of $$2\Omega $$ is connected across one gap of a metrebridge (the length of the wire is $$100\,cm$$ ) and an unknown resistance, greater than $$2\Omega ,$$ is connected across the other gap. When these resistances are interchanged, the balance point shifts by $$20\,cm.$$ Neglecting any corrections, the unknown resistance is
A
$$3\Omega $$
B
$$4\Omega $$
C
$$5\Omega $$
D
$$6\Omega $$
Answer :
$$3\Omega $$
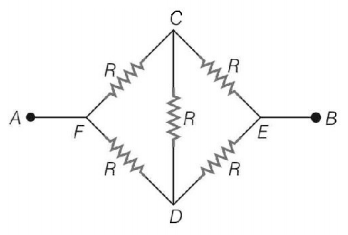
250.
Five equal resistances each of resistance $$R$$ are connected as shown in the figure. A battery of $$4\,V$$ volts is connected between $$A$$ and $$B.$$ The current flowing in $$AFCEB$$ will be
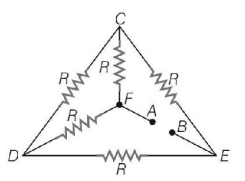
A
$$\frac{{3V}}{R}$$
B
$$\frac{V}{R}$$
C
$$\frac{V}{{2R}}$$
D
$$\frac{{2V}}{R}$$
Answer :
$$\frac{V}{{2R}}$$