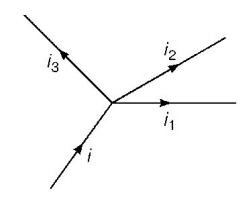
231. Kirchhoff’s first law, i.e. $$\sum i = 0$$ at a junction, deals with the conservation of
A
angular momentum
B
linear momentum
C
energy
D
charge
Answer :
charge
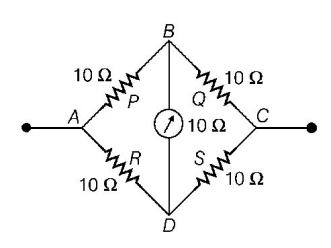
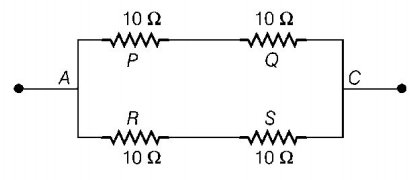
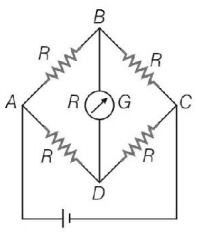
232. In a Wheatstone bridge resistance of each of the four sides is $$10\,\Omega .$$ If the resistance of the galvanometer is also $$10\,\Omega ,$$ then effective resistance of the bridge will be
A
$$10\,\Omega $$
B
$$5\,\Omega $$
C
$$20\,\Omega $$
D
$$40\,\Omega $$
Answer :
$$10\,\Omega $$
233. If a wire is stretched to make it 0.1% longer, its resistance will:
A
increase by 0.2%
B
decrease by 0.2%
C
decrease by 0.05%
D
increase by 0.05%
Answer :
increase by 0.2%
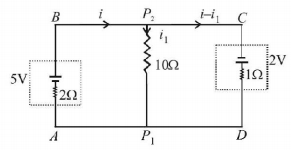
234.
A $$5V$$ battery with internal resistance $$2\,\Omega $$ and a $$2V$$ battery with internal resistance $$1\,\Omega $$ are connected to a $$10\,\Omega $$ resistor as shown in the figure.
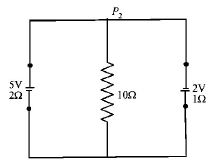
The current in the $$10\,\Omega $$ resistor is
A
$$0.27\,A\,{P_1}$$ to $${P_1}$$
B
$$0.03\,A\,{P_1}$$ to $${P_2}$$
C
$$0.03\,A\,{P_1}$$ to $${P_1}$$
D
$$0.27\,A\,{P_1}$$ to $${P_2}$$
Answer :
$$0.03\,A\,{P_1}$$ to $${P_1}$$
235. In a Wheatstone bridge, all the four arms have equal resistance $$R.$$ If the resistance of the galvanometer arm is also $$R,$$ the equivalent resistance of the combination as seen by the battery is
A
$$R$$
B
$$2\,R$$
C
$$\frac{R}{4}$$
D
$$\frac{R}{2}$$
Answer :
$$R$$
236.
A capacitor is charged using an external battery with a resistance $$x$$ in series. The dashed line shows the variation of In $$I$$ with respect to time. If the resistance is changed to $$2x,$$ the new graph will be
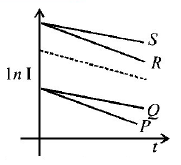
A
$$P$$
B
$$Q$$
C
$$R$$
D
$$S$$
Answer :
$$Q$$
237. The resistance of a discharge tube is
A
zero
B
ohmic
C
non-ohmic
D
infinity
Answer :
non-ohmic
238. A moving coil galvanometer of resistance $$100\,\Omega $$ is used as an ammeter using a resistance $$0.1\,\Omega .$$ The maximum deflection current in the galvanometer is $$100\,\mu A.$$ Find the minimum current in the circuit so that the ammeter shows maximum deflection
A
$$100.1\,mA$$
B
$$1000.1\,mA$$
C
$$10.01\,mA$$
D
$$1.01\,mA$$
Answer :
$$100.1\,mA$$
239. The termistors are usually made of
A
metal oxides with high temperature coefficient of resistivity
B
metals with high temperature coefficient of resistivity
C
metals with low temperature coefficient of resistivity
D
semiconducting materials having low temperature coefficient of resistivity
Answer :
metal oxides with high temperature coefficient of resistivity
240. A cell has an emf $$1.5\,V.$$ When connected across an external resistance of $$2\,\Omega ,$$ the terminal potential difference falls to $$1.0\,V.$$ The internal resistance of the cell is
A
$$2\,\Omega $$
B
$$1.5\,\Omega $$
C
$$1.0\,\Omega $$
D
$$0.5\,\Omega $$
Answer :
$$1.0\,\Omega $$