221. An ideal gas is filled in a closed rigid and thermally insulated container. A coil of $$100\,\Omega $$ resistor carrying current $$1A$$ for 5 minutes supplies heat to the gas. The change in internal energy of the gas is
A
$$10\,kJ$$
B
$$30\,kJ$$
C
$$20\,kJ$$
D
$$0\,kJ$$
Answer :
$$30\,kJ$$
222.
See the electrical circuit shown in this figure. Which of the following equations is a correct equation for it?
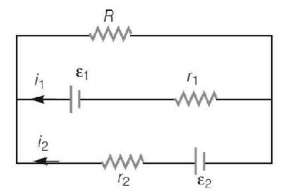
A
$${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R - {i_1}{r_1} = 0$$
B
$${\varepsilon _2} - {i_2}{r_2} - {\varepsilon _1} - {i_1}{r_1} = 0$$
C
$$ - {\varepsilon _2} - \left( {{i_1} + {i_2}} \right)R + {i_2}{r_2} = 0$$
D
$${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R + {i_1}{r_1} = 0$$
Answer :
$${\varepsilon _1} - \left( {{i_1} + {i_2}} \right)R - {i_1}{r_1} = 0$$
223. In electrolysis the mass deposited on an electrode is directly proportional to
A
Current
B
Square of current
C
Concentration of solution
D
Inverse of current
Answer :
Current
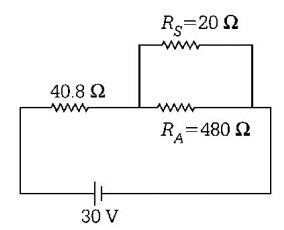
224. A circuit contains an ammeter, a battery of $$30\,V$$ and a resistance $$40.8\,\Omega $$ all connected in series. If the ammeter has a coil of resistance $$480\,\Omega $$ and a shunt of $$20\,\Omega ,$$ then reading in the ammeter will be
A
$$0.5\,A$$
B
$$0.25\,A$$
C
$$2\,A$$
D
$$1\,A$$
Answer :
$$0.5\,A$$
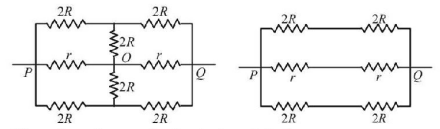
225.
The effective resistance between points $$P$$ and $$Q$$ of the electrical circuit shown in the figure is
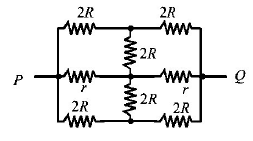
A
$$\frac{{2Rr}}{{R + r}}$$
B
$$\frac{{2R\left( {R + r} \right)}}{{3R + r}}$$
C
$$2r + 4R$$
D
$$\frac{{5R}}{2} + 2r$$
Answer :
$$\frac{{2Rr}}{{R + r}}$$
226. There are three copper wires of length and cross-sectional area $$\left( {L,A} \right),\left( {2L,\frac{A}{2}} \right)\left( {\frac{L}{2},2A} \right).$$ In which case is the resistance minimum ?
A
It is the same in all three cases
B
Wire of cross-sectional area $$2\,A$$
C
Wire of cross-sectional area $$A$$
D
Wire of cross-sectional area $$\frac{1}{2}A$$
Answer :
Wire of cross-sectional area $$2\,A$$
227. If a current is passed through a spring then the spring will
A
expand
B
compress
C
remains same
D
none of these.
Answer :
compress
228. In a large building, there are 15 bulbs of $$40\,W,$$ 5 bulbs of $$100\,W,$$ 5 fans of $$80\,W$$ and 1 heater of $$1\,kW.$$ The voltage of electric mains is $$220\,V.$$ The minimum capacity of the main fuse of the building will be:
A
$$8\,A$$
B
$$10\,A$$
C
$$12\,A$$
D
$$14\,A$$
Answer :
$$12\,A$$
229. Across a metallic conductor of non-uniform cross-section, a constant potential difference is applied. The quantity which remain constant along the conductor is
A
current density
B
current
C
drift velocity
D
electric field
Answer :
current
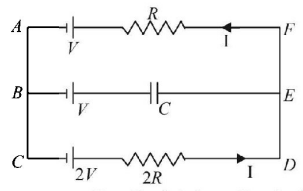
230.
In the given circuit, with steady current, the potential drop across the capacitor must be
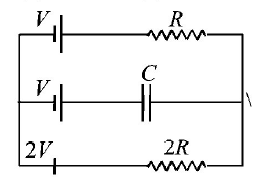
A
$$V$$
B
$$\frac{V}{2}$$
C
$$\frac{V}{3}$$
D
$$\frac{{2V}}{3}$$
Answer :
$$\frac{V}{3}$$