211.
The mass of product liberated on anode in an electrochemical cell depends on
(where $$t$$ is the time period for which the current is passed).
A
$${\left( {It} \right)^{\frac{1}{2}}}$$
B
$$It$$
C
$$\frac{I}{t}$$
D
$${I^2}t$$
Answer :
$$It$$
212.
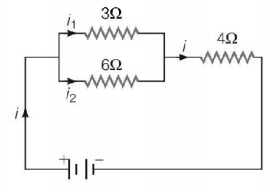
Current through $$3\,\Omega $$ resistor is $$0.8\,A,$$ then potential drop through $$4\,\Omega $$ resistor is
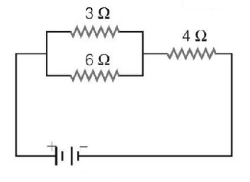
A
$$9.6\,V$$
B
$$2.6\,V$$
C
$$4.8\,V$$
D
$$1.2\,V$$
Answer :
$$4.8\,V$$
213. A battery is charged at a potential of $$15\,V$$ for $$8\,h$$ when the current flowing is $$10\,A.$$ The battery on discharge supplies a current of $$5\,A$$ for $$15\,h.$$ The mean terminal voltage during discharge is $$14\,V.$$ The watt-hour efficiency of the battery is
A
$$82.5\% $$
B
$$80\% $$
C
$$90\% $$
D
$$87.5\% $$
Answer :
$$87.5\% $$
214. Potentiometer measures the potential difference more accurately than a voltmeter, because
A
it has a wire of high resistance
B
it has a wire of low resistance
C
it does not draw current from external circuit
D
it draws a heavy current from external circuit
Answer :
it does not draw current from external circuit
215. A wire when connected to $$220 V$$ mains supply has power dissipation $${P_1}.$$ Now the wire is cut into two equal pieces which are connected in parallel to the same supply. Power dissipation in this case is $${P_2}.$$ Then $${P_2}:{P_1}$$ is
A
1
B
4
C
2
D
3
Answer :
4
216. An energy source will supply a constant current into the load if its internal resistance is
A
very large as compared to the load resistance
B
equal to the resistance of the load
C
non-zero but less than the resistance of the load
D
zero
Answer :
zero
217. A heater coil is cut into two equal parts and only one part is now used in the heater. The heat generated will now be
A
four times
B
doubled
C
halved
D
one fourth
Answer :
doubled
218.
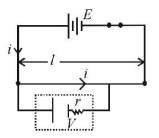
The length of a wire of a potentiometer is $$100\,cm,$$ and the e. m.f. of its standard cell is $$E$$ volt. It is employed to measure the e.m.f. of a battery whose internal resistance is $$0.5\,\Omega $$. If the balance point is obtained at $$1 = 30 cm$$ from the positive end, the e.m.f. of the battery is:
(where $$i$$ is the current in the potentiometer wire.)
A
$$\frac{{30E}}{{100.5}}$$
B
$$\frac{{30E}}{{\left( {100 - 0.5} \right)}}$$
C
$$\frac{{30\left( {E - 0.5i} \right)}}{{100}}$$
D
$$\frac{{30E}}{{100}}$$
Answer :
$$\frac{{30E}}{{100}}$$
219. In a Wheatstone's bridge, three resistances $$P, Q$$ and $$R$$ connected in the three arms and the fourth arm is formed by two resistances $${S_1}$$ and $${S_2}$$ connected in parallel. The condition for the bridge to be balanced will be
A
$$\frac{P}{Q} = \frac{{2R}}{{{S_1} + {S_2}}}$$
B
$$\frac{P}{Q} = \frac{{R\left( {{S_1} + {S_2}} \right)}}{{{S_1}{S_2}}}$$
C
$$\frac{P}{Q} = \frac{{R\left( {{S_1} + {S_2}} \right)}}{{2{S_1}{S_2}}}$$
D
$$\frac{P}{Q} = \frac{R}{{{S_1} + {S_2}}}$$
Answer :
$$\frac{P}{Q} = \frac{{R\left( {{S_1} + {S_2}} \right)}}{{{S_1}{S_2}}}$$
220. A primary cell has an e.m.f. of 1.5 volt. When short-circuited it gives a current of 3 ampere. The internal resistance of the cell is
A
$$4.5\,ohm$$
B
$$2\,ohm$$
C
$$0.5\,ohm$$
D
$$\left( {\frac{1}{{4.5}}} \right){\text{ohm}}$$
Answer :
$$0.5\,ohm$$