181. The electric resistance of a certain wire of iron is $$R.$$ If its length and radius are both doubled, then
A
the resistance will be doubled and the specific resistance will be halved
B
the resistance will be halved and the specific resistance will remain unchanged
C
the resistance will be halved and the specific resistance will be doubled
D
the resistance and the specific resistance will both remain unchanged
Answer :
the resistance will be halved and the specific resistance will remain unchanged
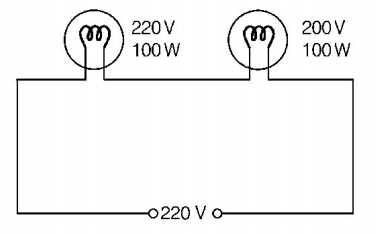
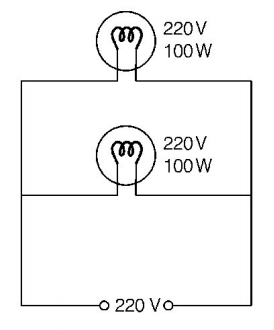
182. Two $$220\,V,100\,W$$ bulbs are connected first in series and then in parallel. Each time the combination is connected to a $$220\,V$$ AC supply line. The power drawn by the combination in each case respectively will be
A
$$200\,W,150\,W$$
B
$$50\,W,200\,W$$
C
$$50\,W,100\,W$$
D
$$100\,W,50\,W$$
Answer :
$$50\,W,200\,W$$
183. A battery is used to charge a parallel plate capacitor till the potential difference between the plates becomes equal to the electromotive force of the battery. The ratio of the energy stored in the capacitor and the work done by the battery will be
A
$$\frac{1}{2}$$
B
$$1$$
C
$$2$$
D
$$\frac{1}{4}$$
Answer :
$$\frac{1}{2}$$
184.
During an experiment with a metre bridge, the galvanometer shows a null point when the jockey is pressed at $$40.0\,cm$$ using a standard resistance of $$90\,\Omega ,$$ as shown in the figure. The least count of the scale used in the metre bridge is $$1mm.$$ The unknown resistance is
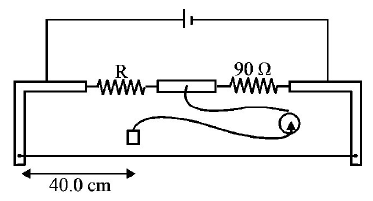
A
$$60 \pm 0.15\,\Omega $$
B
$$135 \pm 0.56\,\Omega $$
C
$$60 \pm 0.25\,\Omega $$
D
$$135 \pm 0.23\,\Omega $$
Answer :
$$60 \pm 0.25\,\Omega $$
185. Incandescent bulbs are designed by keeping in mind that the resistance of their filament increases with the increase in temperature. If at room temperature, $$100\,W,\,60W$$ and $$40\,W$$ bulbs have filament resistances $${R_{100}},{R_{60}}$$ and $${R_{40}},$$ respectively, the relation between these resistances is
A
$$\frac{1}{{{R_{100}}}} = \frac{1}{{{R_{40}}}} + \frac{1}{{{R_{60}}}}$$
B
$${R_{100}} = {R_{40}} + {R_{60}}$$
C
$${R_{100}} > {R_{60}} > {R_{40}}$$
D
$$\frac{1}{{{R_{100}}}} > \frac{1}{{{R_{60}}}} > \frac{1}{{{R_{40}}}}$$
Answer :
$$\frac{1}{{{R_{100}}}} > \frac{1}{{{R_{60}}}} > \frac{1}{{{R_{40}}}}$$
186. The Kirchhoff's second law $$\left( {\Sigma iR = \Sigma E} \right),$$ where the symbols have their usual meanings, is based on
A
conservation of momentum
B
conservation of charge
C
conservation of potential
D
conservation of energy
Answer :
conservation of energy
187.
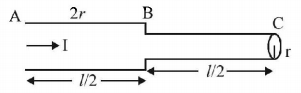
If a steady current $$I$$ is flowing through a cylindrical element $$ABC.$$ Choose the correct relationship
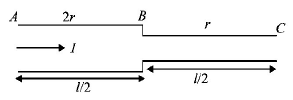
A
$${V_{AB}} = 2{V_{BC}}$$
B
Power across $$BC$$ is 4 times the power across $$AB$$
C
Current densities in $$AB$$ and $$BC$$ are equal
D
Electric field due to current inside $$AB$$ and $$BC$$ are equal
Answer :
Power across $$BC$$ is 4 times the power across $$AB$$
188. $$125\,cm$$ of potentiometer wire balances the emf. of a cell and $$100\,cm$$ of the wire is required for balance, if the poles of the cell are joined by a $$2\Omega $$ resitor. Then the internal resistance of the cell is
A
$$0.25\,\Omega $$
B
$$0.5\,\Omega $$
C
$$0.75\,\Omega $$
D
$$1.25\,\Omega $$
Answer :
$$0.5\,\Omega $$
189.
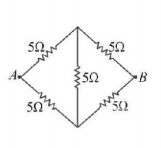
The effective resistance between the terminals $$A$$ and $$B$$ is.
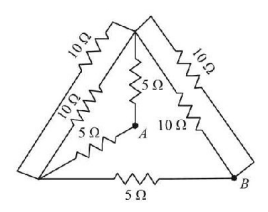
A
$$5\,\Omega $$
B
$$10\,\Omega $$
C
$$15\,\Omega $$
D
$$20\,\Omega $$
Answer :
$$5\,\Omega $$
190.
If in the circuit, power dissipation is $$150\,W,$$ then $$R$$ is
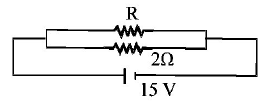
A
$$2\,\Omega $$
B
$$6\,\Omega $$
C
$$5\,\Omega $$
D
$$4\,\Omega $$
Answer :
$$6\,\Omega $$