161. An ammeter reads upto 1 ampere. Its internal resistance is $$0.81\,ohm.$$ To increase the range to $$10\,A$$ the value of the required shunt is
A
$$0.03\,\Omega $$
B
$$0.3\,\Omega $$
C
$$0.3\,\Omega $$
D
$$0.09\,\Omega $$
Answer :
$$0.09\,\Omega $$
162.
A wire of resistance $$R$$ is bent to form a square $$ABCD$$ as shown in the figure. The effective resistance between $$E$$ and $$C$$ is: ($$E$$ is mid-point of arm $$CD$$ )

A
$$R$$
B
$$\frac{7}{{64}}R$$
C
$$\frac{3}{4}R$$
D
$$\frac{1}{{16}}R$$
Answer :
$$\frac{7}{{64}}R$$
163. A thermocouple is made from two metals, Antimony and Bismuth. If one junction of the couple is kept hot and the other is kept cold, then, an electric current will
A
flow from Antimony to Bismuth at the hot junction
B
flow from Bismuth to Antimony at the cold junction
C
now flow through the thermocouple
D
flow from Antimony to Bismuth at the cold junction
Answer :
flow from Antimony to Bismuth at the cold junction
164.
Two batteries of emf $$4\,V$$ and $$8\,V$$ with internal resistance $$1\,\Omega $$ and $$2\,\Omega $$ are connected in a circuit with a resistance of $$9\,\Omega $$ as shown in figure. The current and potential difference between the points $$P$$ and $$Q$$ are

A
$$\frac{1}{3}A$$ and $$3\,V$$
B
$$\frac{1}{6}A$$ and $$4\,V$$
C
$$\frac{1}{9}A$$ and $$9\,V$$
D
$$\frac{1}{12}A$$ and $$12\,V$$
Answer :
$$\frac{1}{3}A$$ and $$3\,V$$
165. A steady current of $$1.5\,A$$ flows through a copper voltameter for $$10\,min.$$ If the electrochemical equivalent of copper is $$30 \times {10^{ - 5}}g{C^{ - 1}},$$ the mass of copper deposited on the electrode will be
A
$$0.40\,g$$
B
$$0.50\,g$$
C
$$0.67\,g$$
D
$$0.27\,g$$
Answer :
$$0.27\,g$$
166. The Kirchhof's first law $$\left( {\sum {i = 0} } \right)$$ and second law $$\left( {\sum {iR = \sum E } } \right)$$ where the symbols have their usual meanings, are respectively based on
A
conservation of charge, conservation of momentum
B
conservation of energy, conservation of charge
C
conservation of momentum, conservation of charge
D
conservation of charge, conservatrion of energy
Answer :
conservation of charge, conservatrion of energy
167. A conductor carries a current of $$50\,\mu A.$$ If the area of cross-section of the conductor is $$50\,m{m^2},$$ then value of the current density in $$A{m^{ - 2}}$$ is
A
$$0.5$$
B
$$1$$
C
$${10^{ - 3}}$$
D
$${10^{ - 6}}$$
Answer :
$$1$$
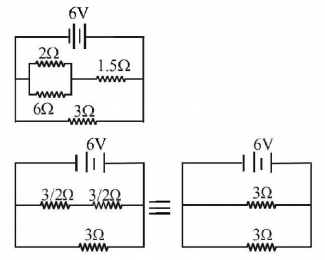
168.
The total current supplied to the circuit by the battery is
A
$$4\,A$$
B
$$2\,A$$
C
$$1\,A$$
D
$$6\,A$$
Answer :
$$4\,A$$
169. A $$5\,A$$ fuse wire can withstand a maximum power of $$1\,W$$ in circuit. The resistance of the fuse wire is
A
$$0.2\,\Omega $$
B
$$5\,\Omega $$
C
$$0.4\,\Omega $$
D
$$0.04\,\Omega $$
Answer :
$$0.04\,\Omega $$
170. A filament bulb $$\left( {500\,W,\,100\,V} \right)$$ is to be used in a $$230\,V$$ main supply. When a resistance $$R$$ is connected in series, it works perfectly and the bulb consumes $$500\,W.$$ The value of $$R$$ is
A
$$230\,\Omega $$
B
$$46\,\Omega $$
C
$$26\,\Omega $$
D
$$13\,\Omega $$
Answer :
$$26\,\Omega $$