81. If in a wire of Young’s modulus $$Y,$$ longitudinal strain $$X$$ is produced, then the value of potential energy stored in its unit volume will be
A
$$Y{X^2}$$
B
$$2Y{X^2}$$
C
$$\frac{{{Y^2}X}}{2}$$
D
$$\frac{{Y{X^2}}}{2}$$
Answer :
$$\frac{{Y{X^2}}}{2}$$
82. Work done in increasing the size of a soap bubble from a radius of $$3 \,cm$$ to $$5 \,cm$$ is nearly (Surface tension of soap solution $$ = 0.03\,N{m^{ - 1}}$$ )
A
$$0.2\pi mJ$$
B
$$2\pi mJ$$
C
$$0.4\pi mJ$$
D
$$4\pi mJ$$
Answer :
$$0.4\pi mJ$$
83. A vessel containing water is given a constant acceleration $$'a'$$ towards the right along a straight horizontal path. Which of the following diagrams represents the surface of the liquid ?
A

B

C
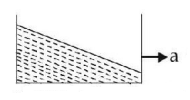

D
None of these
Answer :


84. Water is filled in a container upto height $$3\,m.$$ A small hole of area $$'a\,'$$ is punched in the wall of the container at a height $$52.5 \,cm$$ from the bottom. The cross-sectional area of the container is $$A.$$ If $$\frac{a}{A} = 0.1$$ then $${v^2}$$ is (where $$v$$ is the velocity of water coming out of the hole)-
A
$$50$$
B
$$51$$
C
$$48$$
D
$$51.5$$
Answer :
$$50$$
85.
Consider four steel wires of dimensions given below ($$d =$$ diameter and $$l =$$ length) :
$$\eqalign{
& \left( A \right)\,l = 1m,d = 1\,mm\,\left( B \right)\,l = 2m,d = 2\,mm \cr
& \left( C \right)\,l = 2m,d = 1\,mm\,\left( D \right)\,l = 1m,d = 2\,mm \cr} $$
If same force is applied to all the wires then the elastic potential energy stored will be maximum in wire:
A
$$A$$
B
$$B$$
C
$$C$$
D
$$D$$
Answer :
$$C$$
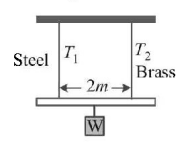
86.
A light rod of length $$2m$$ suspended from the ceiling horizontally by means of two vertical wires of equal length. A weight $$W$$ is hung from a light rod as shown in figure. The rod hung by means of a steel wire of cross-sectional area $${A_1} = 0.1\,c{m^2}$$ and brass wire of cross- sectional area $${A_2} = 0.2\,c{m^2}.$$ To have equal stress in both wires, $$\frac{{{T_1}}}{{{T_2}}} = $$
A
$$\frac{1}{3}$$
B
$$\frac{1}{4}$$
C
$$\frac{4}{3}$$
D
$$\frac{1}{2}$$
Answer :
$$\frac{1}{2}$$
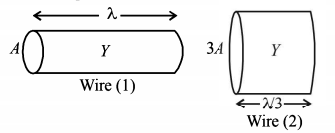
87. Two wires are made of the same material and have the same volume. However wire $$1$$ has cross-sectional area $$A$$ and wire $$2$$ has cross-sectional area $$3A.$$ If the length of wire $$1$$ increases by $$\Delta x$$ on applying force $$F ,$$ how much force is needed to stretch wire $$2$$ by the same amount?
A
$$4\,F$$
B
$$6\,F$$
C
$$9\,F$$
D
$$F\,$$
Answer :
$$9\,F$$
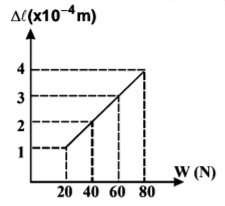
88.
The adjacent graph shows the extension $$\left( {\Delta \ell } \right)$$ of a wire of length $$1 \,m$$ suspended from the top of a roof at one end and with a load $$W$$ connected to the other end. If the cross-sectional area of the wire is $${10^{ - 6}}{m^2},$$ calculate the Young’s modulus of the material of the wire.
A
$$2 \times {10^{11}}N/m$$
B
$$2 \times {10^{ - 11}}N/m$$
C
$$2 \times {10^{ - 12}}N/m$$
D
$$2 \times {10^{ - 13}}N/m$$
Answer :
$$2 \times {10^{11}}N/m$$
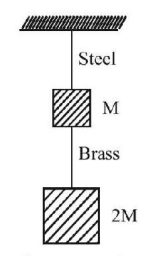
89.
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are $$a,b$$ and $$c$$ respectively, then the corresponding ratio of increase in their lengths is:
A
$$\frac{{3c}}{{2a{b^2}}}$$
B
$$\frac{{2{a^2}c}}{b}$$
C
$$\frac{{3a}}{{2{b^2}c}}$$
D
$$\frac{{2ac}}{{{b^2}}}$$
Answer :
$$\frac{{3a}}{{2{b^2}c}}$$
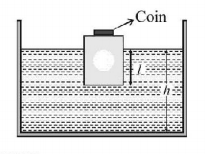
90.
A wooden block, with a coin placed on its top, floats in water as shown in fig. the distance $$l$$ and $$h$$ are shown there. After some time the coin falls into the water. Then
A
$$\ell $$ decreases and $$h$$ increases
B
$$\ell $$ increases and $$h$$ decreases
C
both $$\ell $$ and $$h$$ increases
D
both $$\ell $$ and $$h$$ decreases
Answer :
both $$\ell $$ and $$h$$ decreases