91. A wire fixed at the upper end stretches by length $$\ell $$ by applying a force $$F .$$ The work done in stretching is-
A
$$2F\ell $$
B
$$F\ell $$
C
$$\frac{F}{{2\ell }}$$
D
$$\frac{{F\ell }}{2}$$
Answer :
$$\frac{{F\ell }}{2}$$
92. If a ball of steel (density $$\rho = 7.8\,g\,c{m^{ - 3}}$$ ) attains a terminal velocity of $$10\,cm{s^{ - 1}}$$ when falling in a tank of water (coefficient of viscosity $${\eta _{{\text{water}}}} = 8.5 \times {10^{ - 4}}\,Pa - s$$ ) then its terminal velocity in glycerine $$\left( {\rho = 12\,g\,c{m^{ - 3}},\eta = 13.2\,Pa - s} \right)$$ would be nearly
A
$$1.6 \times {10^{ - 5}}cm{s^{ - 1}}$$
B
$$6.25 \times {10^{ - 4}}cm{s^{ - 1}}$$
C
$$6.45 \times {10^{ - 4}}cm{s^{ - 1}}$$
D
$$1.5 \times {10^{ - 5}}cm{s^{ - 1}}$$
Answer :
$$6.25 \times {10^{ - 4}}cm{s^{ - 1}}$$
93. A rubber cord catapult has cross-sectional area $$25\,m{m^2}$$ and initial length of rubber cord is $$10\,cm.$$ It is stretched to $$5\,cm$$ and then released to project a missile of mass $$5\,gm.$$ Taking $${Y_{{\text{rubber}}}} = 5 \times {10^8}\,N/{m^2}.$$ Velocity of projected missile is
A
$$20\,m{s^{ - 1}}$$
B
$$100\,m{s^{ - 1}}$$
C
$$250\,m{s^{ - 1}}$$
D
$$200\,m{s^{ - 1}}$$
Answer :
$$250\,m{s^{ - 1}}$$
94. A solid sphere of radius $$r$$ made of a soft material of bulk modulus $$K$$ is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross-section of cylindrical container. When a mass $$m$$ is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere $$\left( {\frac{{dr}}{r}} \right),$$ is-
A
$$\frac{{Ka}}{{mg}}$$
B
$$\frac{{Ka}}{{3mg}}$$
C
$$\frac{{mg}}{{3Ka}}$$
D
$$\frac{{mg}}{{Ka}}$$
Answer :
$$\frac{{mg}}{{3Ka}}$$
95. A thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If $${\rho _c}$$ is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is-
A
more than half-filled if $${\rho _c}$$ is less than $$0.5.$$
B
more than half-filled if $${\rho _c}$$ is more than $$1.0.$$
C
half-filled if $${\rho _c}$$ is more than $$0.5.$$
D
less than half-filled if $${\rho _c}$$ is less than $$0.5.$$
Answer :
more than half-filled if $${\rho _c}$$ is less than $$0.5.$$
96. A rectangular film of liquid is extended from $$\left( {4\,cm \times 2\,cm} \right)$$ to $$\left( {5\,cm \times 4 \times cm} \right).$$ If the work done is $$3 \times {10^{ - 4}}J,$$ the value of the surface tension of the liquid is
A
$$0.250\,N{m^{ - 1}}$$
B
$$0.125\,N{m^{ - 1}}$$
C
$$0.2\,N{m^{ - 1}}$$
D
$$8.0\,N{m^{ - 1}}$$
Answer :
$$0.125\,N{m^{ - 1}}$$
97. A cylinderical vessel contains a liquid of density $$\rho $$ filled upto a height $$h.$$ The upper surface of the liquid is in contact with a piston of mass $$m$$ and area of cross-section $$A.$$ A small hole is drilled at the bottom of the vessel. (Neglect the viscous effects) The speed with which the liquid comes out of the hole is :
A
$$\sqrt 2 gh$$
B
$$\sqrt {2g\left( {h + \frac{m}{{\rho A}}} \right)} $$
C
$$\sqrt {g\left( {h + \frac{m}{{\rho A}}} \right)} $$
D
$$\sqrt {g\left( {h + \frac{{2m}}{{\rho A}}} \right)} $$
Answer :
$$\sqrt {2g\left( {h + \frac{m}{{\rho A}}} \right)} $$
98. A spherical ball contracts in volume by $$0.02\% $$ when subjected to a pressure of $$100$$ atmosphere. Assuming one atmosphere $$ = {10^5}N{m^{ - 2}},$$ the bulk modulus of the material of the ball is
A
$$0.02 \times {10^5}N/{m^2}$$
B
$$0.02 \times {10^7}N/{m^2}$$
C
$$50 \times {10^7}N/{m^2}$$
D
$$50 \times {10^9}N/{m^2}$$
Answer :
$$50 \times {10^9}N/{m^2}$$
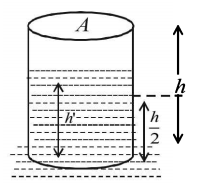
99.
For the arrangement shown in the figure, find the time interval in seconds after which the water jet ceases to cross the wall. Area of the cross section of the tank $$A = \sqrt 5 {m^2}$$ and area of the orifice $$a = 4\,c{m^2}.$$ [Assume that the container remaining fixed]

A
$$1000s$$
B
$$2000s$$
C
$$1500s$$
D
$$500s$$
Answer :
$$1000s$$
100. Two soap bubbles of radii $$a$$ and $$b$$ combine to forma single bubble of radius $$c.$$ If $$P$$ is the external pressure, then the surface tension of the soap solution is
A
$$\frac{{P\left( {{c^3} + {a^3} + {b^3}} \right)}}{{4\left( {{a^2} + {b^2} - {c^2}} \right)}}$$
B
$$\frac{{P\left( {{c^3} - {a^3} - {b^3}} \right)}}{{4\left( {{a^2} + {b^2} - {c^2}} \right)}}$$
C
$$P{c^3} - 4{a^2} - 4{b^2}$$
D
$$P{c^2} - 2{a^2} - 3{b^2}$$
Answer :
$$\frac{{P\left( {{c^3} - {a^3} - {b^3}} \right)}}{{4\left( {{a^2} + {b^2} - {c^2}} \right)}}$$