51. A vertical metal cylinder of radius $$2\,cm$$ and length $$2\,m$$ is fixed at the lower end and a load of $$100\,kg$$ is put on it. Find the strain. [Young's modulus of the metal $$ = 2 \times {10^{11}}N/{m^2}$$ ]
A
$$4 \times {10^{ - 6}}$$
B
$$3 \times {10^{ - 8}}$$
C
$$2 \times {10^{ - 9}}$$
D
$$6 \times {10^{ - 8}}$$
Answer :
$$4 \times {10^{ - 6}}$$
52. An air bubble of radius $$1\,cm$$ rises with terminal velocity $$0.21\,cm/s$$ in liquid column. If the density of liquid is $$1.47 \times {10^3}\,kg/{m^3}.$$ Then the value of coefficient of viscosity of liquid ignoring the density of air, will be
A
$$1.71 \times {10^4}{\text{poise}}$$
B
$$1.82 \times {10^4}{\text{poise}}$$
C
$$1.78 \times {10^4}{\text{poise}}$$
D
$$1.52 \times {10^4}{\text{poise}}$$
Answer :
$$1.52 \times {10^4}{\text{poise}}$$
53.
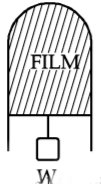
A thin liquid film formed between a U-shaped wire and a light slider supports a weight of $$1.5 \times {10^{ - 2}}N$$ (see figure). The length of the slider is $$30 \,cm$$ and its weight negligible. The surface tension of the liquid film is-
A
$$0.0125\,N{m^{ - 1}}$$
B
$$0.1\,N{m^{ - 1}}$$
C
$$0.05\,N{m^{ - 1}}$$
D
$$0.025\,N{m^{ - 1}}$$
Answer :
$$0.025\,N{m^{ - 1}}$$
54. Three liquids of densities $${\rho _1},{\rho _2}$$ and $${\rho _3}$$ (with $${\rho _1} > {\rho _2} > {\rho _3}$$ ), having the same value of surface tension $$T,$$ rise to the same height in three identical capillaries. The angles of contact $${\theta _1},{\theta _2}$$ and $${\theta _3}$$ obey
A
$$\frac{\pi }{2} > {\theta _1} > {\theta _2} > {\theta _3} \geqslant 0$$
B
$$0 \leqslant {\theta _1} < {\theta _2} < {\theta _3} < \frac{\pi }{2}$$
C
$$\frac{\pi }{2} < {\theta _1} < {\theta _2} < {\theta _3} < \pi $$
D
$$\pi > {\theta _1} > {\theta _2} > {\theta _3} > \frac{\pi }{2}$$
Answer :
$$0 \leqslant {\theta _1} < {\theta _2} < {\theta _3} < \frac{\pi }{2}$$
55. Air flows horizontally with a speed $$v = 106\,km/hr.$$ A house has plane roof of area $$A = 20\,{m^2}.$$ The magnitude of aerodynamic lift of the roof is
A
$$1.127 \times {10^4}N$$
B
$$5.0 \times {10^4}N$$
C
$$1.127 \times {10^5}N$$
D
$$3.127 \times {10^4}N$$
Answer :
$$1.127 \times {10^4}N$$
56. The velocity of water in a river is $$18\,km/hr$$ near the surface. If the river is $$5\,m$$ deep, find the shearing stress between the horizontal layers of water. The co-efficient of viscosity of water $$ = {10^{ - 2}}{\text{poise}}{\text{.}}$$
A
$${10^{ - 1}}N/{m^2}$$
B
$${10^{ - 2}}N/{m^2}$$
C
$${10^{ - 3}}N/{m^2}$$
D
$${10^{ - 4}}N/{m^2}$$
Answer :
$${10^{ - 2}}N/{m^2}$$
57. A sphere of solid material of specific gravity 8 has a concentric spherical cavity and just sinks in water. The ratio of radius of cavity to that of outer radius of the sphere must be
A
$$\frac{{{7^{\frac{1}{3}}}}}{2}$$
B
$$\frac{{{5^{\frac{1}{3}}}}}{2}$$
C
$$\frac{{{9^{\frac{1}{3}}}}}{2}$$
D
$$\frac{{{3^{\frac{1}{3}}}}}{2}$$
Answer :
$$\frac{{{7^{\frac{1}{3}}}}}{2}$$
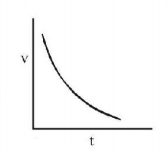
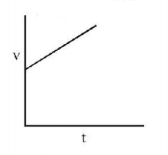
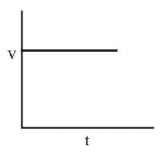
58. Which of the following is the velocity time graph of a small spherical body falling through a long columns of a viscous liquid?
A

B

C

D
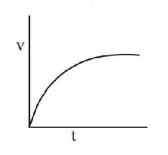

Answer :


59.
An incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity $$'v'$$ of the fluid is
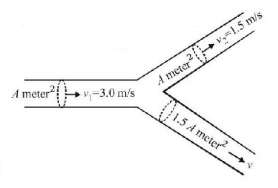
A
$$3.0\,m/s$$
B
$$1.5\,m/s$$
C
$$1.0\,m/s$$
D
$$2.25\,m/s$$
Answer :
$$1.0\,m/s$$
60.
In the arrangement as shown, $${m_B} = 3m,$$ density of liquid is $$r$$ and density of block $$B$$ is $$2\rho .$$ The system is released from rest so that block $$B$$ moves up when in liquid and moves down when out of liquid with the same acceleration. Find the mass of block $$A.$$
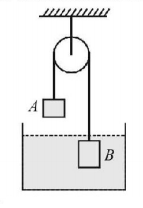
A
$$\frac{7}{4}m$$
B
$$2m$$
C
$$\frac{9}{2}m$$
D
$$\frac{9}{4}m$$
Answer :
$$\frac{9}{4}m$$