31. Copper of fixed volume $$V$$ is drawn into wire of length $$l.$$ When this wire is subjected to a constant force $$F,$$ the extension produced in the wire is $$\Delta l.$$ Which of the following graphs is a straight line?
A
$$\Delta l\,versus\,\frac{1}{l}$$
B
$$\Delta l\,versus\,{l^2}$$
C
$$\Delta l\,versus\,\frac{1}{{{l^2}}}$$
D
$$\Delta l\,versus\,l$$
Answer :
$$\Delta l\,versus\,{l^2}$$
32. Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of $${30^ \circ }$$ with each other. When suspended in a liquid of density $$0.8g\,c{m^{ - 3}},$$ the angle remains the same. If density of the material of the sphere is $$1.6g\,c{m^{ - 3}},$$ the dielectric constant of the liquid is-
A
$$4$$
B
$$3$$
C
$$2$$
D
$$1$$
Answer :
$$2$$
33.
In the figure shown, a light container is kept on a horizontal rough surface of coefficient of friction $$\mu = \frac{{Sh}}{V}.$$ A very small hole of area $$S$$ is made at depth $$h.$$ Water of volume $$V$$ is filled in the container. The friction is not sufficient to keep the container at rest. The acceleration of the container initially is
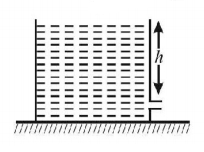
A
$$\frac{V}{{Sh}}g$$
B
$$g$$
C
zero
D
$$\frac{{Sh}}{V}g$$
Answer :
$$\frac{{Sh}}{V}g$$
34. The length of elastic string, obeying Hooke’s law is $${\ell _1}$$ metres when the tension $$4N$$ and $${\ell _2}$$ metres when the tension is $$5N.$$ The length in metres when the tension is $$9N$$ is -
A
$$5{\ell _1} - 4{\ell _2}$$
B
$$5{\ell _2} - 4{\ell _1}$$
C
$$9{\ell _1} - 8{\ell _2}$$
D
$$9{\ell _2} - 8{\ell _1}$$
Answer :
$$5{\ell _2} - 4{\ell _1}$$
35. A steel ring of radius $$r$$ and cross-section area $$'A'$$ is fitted on to a wooden disc of radius $$R\left( {R > r} \right).$$ If Young's modulus be $$E,$$ then the force with which the steel ring is expanded is
A
$$AE\frac{R}{r}$$
B
$$AE\left( {\frac{{R - r}}{r}} \right)$$
C
$$\frac{E}{A}\left( {\frac{{R - r}}{A}} \right)$$
D
$$\frac{{Er}}{{AR}}$$
Answer :
$$AE\left( {\frac{{R - r}}{r}} \right)$$
36. which of the following is correct for young's modulus of elasticity $$\left( \gamma \right)$$ ? [where $$r$$ = radius of cross section of wire, $$l$$ = length of wire]
A
$$\gamma \propto {r^2}$$
B
$$\gamma \propto {l^3}$$
C
$$\gamma \propto \frac{1}{{{r^2}}}$$
D
$$\gamma \propto {l^2}$$
Answer :
$$\gamma \propto \frac{1}{{{r^2}}}$$
37. The cylindrical tube of a spray pump has radius $$R,$$ one end of which has $$n$$ fine holes, each of radius $$r.$$ If the speed of the liquid in the tube is $$v,$$ the speed of the ejection of the liquid through the holes is
A
$$\frac{{v{R^2}}}{{{n^2}{r^2}}}$$
B
$$\frac{{v{R^2}}}{{n{r^2}}}$$
C
$$\frac{{v{R^2}}}{{{n^3}{r^2}}}$$
D
$$\frac{{{v^2}R}}{{nr}}$$
Answer :
$$\frac{{v{R^2}}}{{n{r^2}}}$$
38. Which of the following affects the elasticity of a substance?
A
Change in temperature
B
Hammering and annealing
C
Impurity in substance
D
All of the above
Answer :
All of the above
39. Air of density $$1.2\,kg\,{m^{ - 3}}$$ is blowing across the horizontal wings of an aeroplane in such a way that its speeds above and below the wings are $$150\,m{s^{ - 1}}$$ and $$100\,m{s^{ - 1}},$$ respectively. The pressure difference between the upper and lower sides of the wings, is
A
$$60\,N{m^{ - 2}}$$
B
$$180\,N{m^{ - 2}}$$
C
$$7500\,N{m^{ - 2}}$$
D
$$12500\,N{m^{ - 2}}$$
Answer :
$$7500\,N{m^{ - 2}}$$
40. When temperature of a gas is $${20^ \circ }C$$ and pressure is changed from $${p_1} = 1.01 \times {10^5}Pa$$ to $${p_2} = 1.165 \times {10^5}Pa$$ then the volume changed by $$10\% .$$ The bulk modulus is-
A
$$1.55 \times {10^5}Pa$$
B
$$0.115 \times {10^5}Pa$$
C
$$1.4 \times {10^5}Pa$$
D
$$1.01 \times {10^5}Pa$$
Answer :
$$1.55 \times {10^5}Pa$$
.PNG)
