11. A wire suspended vertically from one of its ends is stretched by attaching a weight of $$200\,N$$ to the lower end. The weight stretches the wire by $$1\,mm.$$ Then the elastic energy stored in the wire is
A
$$0.2\,J$$
B
$$10\,J$$
C
$$20\,J$$
D
$$0.1\,J$$
Answer :
$$0.1\,J$$
12. A steel wire and a copper wire of equal length and equal cross-sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of the stresses developed in the two wires and $$Y$$ of steel $$ = 2 \times {10^{11}}\,N/{m^2}.$$ $$Y$$ of copper $$ = 1.3 \times {10^{11}}\,N/{m^2}.$$
A
1
B
3
C
5
D
7
Answer :
1
13.
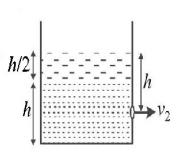
Equal volumes of two immiscible liquids of densities $$\rho $$ and $$2\rho $$ are filled in a vessel as shown in figure. Two small holes are punched at depth $$\frac{h}{2}$$ and $$\frac{3h}{2}$$ from the surface of lighter liquid. If $${v_1}$$ and $${v_2}$$ are the velocities of a flux at these two holes, then $$\frac{{{v_1}}}{{{v_2}}}$$ is
A
$$\frac{1}{{2\sqrt 2 }}$$
B
$$\frac{1}{2}$$
C
$$\frac{1}{4}$$
D
$$\frac{1}{{\sqrt 2 }}$$
Answer :
$$\frac{1}{{\sqrt 2 }}$$
14.
When a $$4\,kg$$ mass is hung vertically on a light spring that obeys Hooke’s law, the spring stretches by $$2\,cms.$$ The work required to be done by an external agent in stretching this spring by $$5\,cms$$ will be
$$\left( {g = 9.8\,m/{{\sec }^2}} \right)$$
A
4.900 joule
B
2.450 joule
C
0.495 joule
D
0.245 joule
Answer :
2.450 joule
15. A uniform cube is subjected to volume compression. If each side is decreased by $$1\% ,$$ then bulk strain is
A
0.01
B
0.06
C
0.02
D
0.03
Answer :
0.03
16. A small spherical ball falling through a viscous medium of negligible density has terminal velocity $$v.$$ Another ball of the same mass but of radius twice that of the earlier falling through the same viscous medium will have terminal velocity
A
$$v$$
B
$$\frac{v}{4}$$
C
$$\frac{v}{2}$$
D
$$2v$$
Answer :
$$\frac{v}{2}$$
17. A force of $$6 \times {10^6}\,N{m^{ - 2}}$$ is required for breaking a material. Then density $$\rho $$ of the material is $$3 \times {10^3}\,kg\,{m^{ - 3}}.$$ If the wire is to break under its own weight, the length of the wire made of that material should be (take $$g = 10\,m{s^{ - 2}}$$ )
A
$$20\,m$$
B
$$200\,m$$
C
$$100\,m$$
D
$$2000\,m$$
Answer :
$$200\,m$$
18. A copper wire of length $$1.0\,m$$ and a steel wire of length $$0.5\,m$$ having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by $$1\,mm.$$ If the Young’s modulii of copper and steel are respectively $$1.0 \times {10^{11}}N{m^{ - 2}}$$ and $$2.0 \times {10^{11}}N{m^{ - 2}},$$ the total extension of the composite wire is :
A
$$1.75\,mm$$
B
$$2.0\,mm$$
C
$$1.50\,mm$$
D
$$1.25\,mm$$
Answer :
$$1.25\,mm$$
19.
A container filled with viscous liquid is moving vertically downwards with constant speed $$3{v_0}.$$ At the instant shown, a sphere of radius $$r$$ is moving vertically downwards (in liquid) has speed $${v_0}.$$ The coefficient of viscosity is $$\eta .$$ There is no relative motion between the liquid and the container. Then at the shown instant, the magnitude of viscous force acting on sphere is
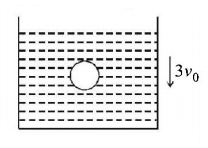
A
$$6\pi \eta r{v_0}$$
B
$$12\pi \eta r{v_0}$$
C
$$18\pi \eta r{v_0}$$
D
$$24\pi \eta r{v_0}$$
Answer :
$$12\pi \eta r{v_0}$$
20.
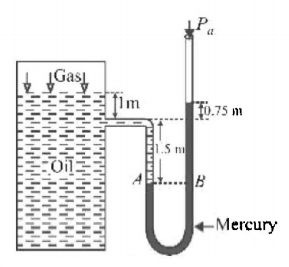
What is the absolute pressure of the gas above the liquid surface in the tank shown in fig. Density of oil $$ = 820\,kg/{m^3},$$ density of mercury $$ = 13.6 \times {10^3}\,kg/{m^3}.$$ Given 1 atmospheric pressure $$ = 1.01 \times {10^5}\,N/{m^2}.$$
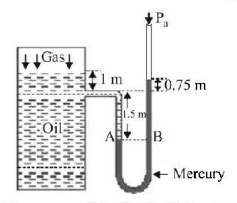
A
$$3.81 \times {10^5}\,N/{m^2}$$
B
$$6 \times {10^6}\,N/{m^2}$$
C
$$5 \times {10^7}\,N/{m^2}$$
D
$$4.6 \times {10^2}\,N/{m^2}$$
Answer :
$$3.81 \times {10^5}\,N/{m^2}$$