181. A reaction attains equilibrium state under standard conditions, then what is incorrect for this ?
A
Equilibrium constant $$K = 0$$
B
Equilibrium constant $$K = 1$$
C
$$\Delta {G^ \circ } = 0$$ and $$\Delta {H^ \circ } = T\Delta {S^ \circ }$$
D
$$\Delta G = 0$$ and $$\Delta H = T\Delta S$$
Answer :
Equilibrium constant $$K = 0$$
182.
What will be the heat of reaction for the following reaction ? Will the reaction be exothermic or endothermic ?
$$\eqalign{
& F{e_2}{O_{3\left( s \right)}} + 3{H_{2\left( g \right)}} \to 2F{e_{\left( s \right)}} + 3{H_2}{O_{\left( l \right)}} \cr
& {\Delta _f}{H^ \circ }\left( {{H_2}O,l} \right) = - 285.83\,kJ\,mo{l^{ - 1}}, \cr
& {\Delta _f}{H^ \circ }\left( {F{e_2}{O_3},s} \right) = - 824.2\,kJ\,mo{l^{ - 1}} \cr} $$
A
$$ - 824.2\,kJ\,mo{l^{ - 1}},{\text{exothermic}}$$
B
$$ + 33.3\,kJ\,mo{l^{ - 1}},{\text{endothermic}}$$
C
$$ - 33.3\,kJ\,mo{l^{ - 1}},{\text{exothermic}}$$
D
$$ + 824.2\,kJ\,mo{l^{ - 1}},{\text{endothermic}}$$
Answer :
$$ - 33.3\,kJ\,mo{l^{ - 1}},{\text{exothermic}}$$
183. Which of the following relationships is not correct for the relation between $$\Delta H$$ and $$\Delta U?$$
A
When $$\Delta {n_g} = 0$$ then $$\Delta H = \Delta U$$
B
When $$\Delta {n_g} > 0$$ then $$\Delta H > \Delta U$$
C
When $$\Delta {n_g} < 0$$ then $$\Delta H < \Delta U$$
D
When $$\Delta {n_g}RT = 0$$ then $$\Delta H > \Delta U$$
Answer :
When $$\Delta {n_g}RT = 0$$ then $$\Delta H > \Delta U$$
184. Equal volumes of molar hydrochloric acid and sulphuric acid are neutralised by dilute $$NaOH$$ solution and $$x$$ $$kcal$$ and $$y$$ $$kcal$$ of heat are liberated respectively. Which of the following is true?
A
$$x = y$$
B
$$x = \frac{1}{2}y$$
C
$$x = 2y$$
D
$${\text{None of the above}}$$
Answer :
$$x = \frac{1}{2}y$$
185.
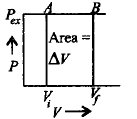
Work done on an ideal gas in a cylinder when it is compressed by an external pressure in a single step is shown below :
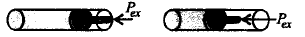
Which of the following graphs will show the work done on the gas ?
A
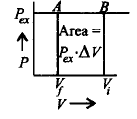

B
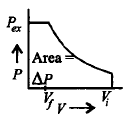

C
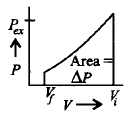

D

Answer :


186.
Diborane is a potential rocket fuel which undergoes combustion according to the equation $${B_2}{H_6}\left( g \right) + 3{O_2}\left( s \right) \to $$ $${B_2}{O_3}\left( s \right) + 3{H_2}O\left( g \right)$$ Calculate the enthalpy change for the combustion of diborane. Given
$$\left( {\text{i}} \right)\,2B\left( s \right) + \frac{3}{2}{O_2}\left( g \right) \to $$ $${B_2}{O_3}\left( s \right);\Delta H = - 1273\,kJ\,{\text{per }}mol$$
$$\left( {{\text{ii}}} \right){H_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to $$ $${H_2}O\left( l \right);\Delta H = - 286\,kJ\,{\text{per}}\,mol$$
$$\left( {{\text{iii}}} \right)\,{H_2}O\left( l \right) \to {H_2}O\left( g \right);$$ $$\Delta H = 44\,kJ\,{\text{per}}\,mol$$
$$\left( {{\text{iv}}} \right)\,2B\left( s \right) + 3{H_2}\left( g \right) \to $$ $${B_2}{H_6}\left( g \right);\Delta H = 36\,kJ\,{\text{per}}\,mol$$
A
$$ + 2035\,kJ\,{\text{per}}\,mol$$
B
$$ - 2035\,kJ\,{\text{per}}\,mol$$
C
$$ + 2167\,kJ\,{\text{per}}\,mol$$
D
$$ - 2167\,kJ\,{\text{per}}\,mol$$
Answer :
$$ - 2035\,kJ\,{\text{per}}\,mol$$
187. For a reaction, $$2{K_{\left( g \right)}} + {L_{\left( g \right)}} \to 2{M_{\left( g \right)}};\Delta {U^ \circ } = - 10.5\,kJ$$ and $$\Delta {S^ \circ } = - 44.1\,J\,{K^{ - 1}}.$$ Calculate $$\Delta {G^ \circ }$$ for the reaction and predict whether the reaction will be spontaneous or non-spontaneous ?
A
$$\Delta G = 0.16\,kJ,{\text{non - spontaneous}}$$
B
$$\Delta G = - 0.16\,kJ,{\text{spontaneous}}$$
C
$$\Delta G = + 26.12\,kJ,{\text{non - spontaneous}}$$
D
$$\Delta G = - 26.12\,kJ,{\text{spontaneous}}$$
Answer :
$$\Delta G = 0.16\,kJ,{\text{non - spontaneous}}$$
188. Enthalpy of neutralisation of $$HCl$$ with $$NaOH$$ is $$x.$$ The heat evolved when $$500\,mL$$ of $$2\,N\,HCl$$ are mixed with $$250\,mL$$ of $$4N\,NaOH$$ will be.
A
500$$\,x$$
B
100$$\,x$$
C
$$x$$
D
10$$\,x$$
Answer :
$$x$$
189.
Which of the following lines correctly show the temperature dependence of equilibrium constant, $$K,$$ for an exothermic reaction?

A
A and B
B
B and C
C
C and D
D
A and D
Answer :
A and B
190. Which of the following reactions will have the value of enthalpy of neutralisation as $$ - 57.1\,kJ\,mo{l^{ - 1}}?$$
A
$$C{H_3}COOH + NaOH \to C{H_3}COONa + {H_2}O$$
B
$$HCl + NaOH \to NaCl + {H_2}O$$
C
$$HCl + N{H_4}OH \to N{H_4}Cl + {H_2}O$$
D
$$HCOOH + NaOH \to HCOONa + {H_2}O$$
Answer :
$$HCl + NaOH \to NaCl + {H_2}O$$