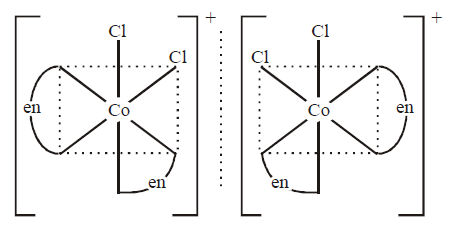
301. Which of the following complex ions will exhibit optical isomerism ? $$\left( {en = 1,2{\text{ - diamine ethane}}} \right).$$
A
$${\left[ {Cr{{\left( {N{H_3}} \right)}_2}C{l_2}} \right]^ + }$$
B
$${\left[ {Co{{\left( {en} \right)}_2}C{l_2}} \right]^ + }$$
C
$${\left[ {Co{{\left( {N{H_3}} \right)}_4}C{l_2}} \right]^ + }$$
D
$${\left[ {Zn{{\left( {en} \right)}_2}} \right]^{2 + }}$$
Answer :
$${\left[ {Co{{\left( {en} \right)}_2}C{l_2}} \right]^ + }$$
302. The IUPAC name of the coordination compound $${K_3}\left[ {Fe{{\left( {CN} \right)}_6}} \right]$$ is
A
Tripotassium hexacyanoiron (II)
B
Potassium hexacyanoiron (II)
C
Potassium hexacyanoferrate (III)
D
Potassium hexacyanoferrate (II)
Answer :
Potassium hexacyanoferrate (III)
303. When $$Hg{I_2}$$ is added to excess of aqueous $$KI,$$ mercury largely exists as.
A
$$H{g_2}{I_2}$$
B
$${\left[ {Hg{I_3}} \right]^ - }$$
C
$${\left[ {Hg{I_4}} \right]^{2 - }}$$
D
$${\text{none of these}}$$
Answer :
$${\left[ {Hg{I_4}} \right]^{2 - }}$$
304.
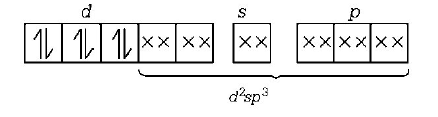
Which one of the following is an inner orbital complex as well as diamagnetic in behaviour ?
$$\left( {{\text{At}}{\text{. no}}{\text{. of}}\,\,Zn = 30,Cr = 24,Co = 27,Ni = 28} \right)$$
A
$${\left[ {Zn{{\left( {N{H_3}} \right)}_6}} \right]^{2 + }}$$
B
$${\left[ {Cr{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }}$$
C
$${\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }}$$
D
$${\left[ {Ni{{\left( {N{H_3}} \right)}_6}} \right]^{2 + }}$$
Answer :
$${\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }}$$
305. The shape of $${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$ is
A
tetrahedral
B
square planar
C
pyramidal
D
octahedral
Answer :
square planar
306. Two complexes $$\left[ {Cr\left( {{H_2}{O_6}} \right)} \right]C{l_3}\left( A \right)\,{\text{and}}\,\left[ {Cr{{\left( {N{H_3}} \right)}_6}} \right]C{l_3}\left( B \right)$$ are violet and yellow coloured, respectively. The incorrect statement regarding them is:
A
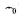 values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
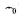 values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively. B
both are paramagnetic with three unpaired electrons.
C
both absorb energies corresponding to their complementary colors.
D
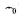 value for $$\left( A \right)$$ is less than that $$\left( B \right).$$
value for $$\left( A \right)$$ is less than that $$\left( B \right).$$
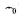 value for $$\left( A \right)$$ is less than that $$\left( B \right).$$
value for $$\left( A \right)$$ is less than that $$\left( B \right).$$
Answer :
 values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
 values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively.
values of $$\left( A \right)\,{\text{and}}\,\left( B \right)$$ are calculated from the energies of biolet and yellow light, respectively. 307. Which of the following is correct?
A
Valence bond theory explains the colour of the coordination compounds.
B
$${\left[ {NiC{l_4}} \right]^{2 - }}$$ is diamagnetic in nature.
C
Ambident ligands can show linkage isomerism.
D
A bidentate ligand can have four coordination
sites.
Answer :
Ambident ligands can show linkage isomerism.
308. In $$Fe{\left( {CO} \right)_5},\,{\text{the}}\,Fe - C\,$$ bond possesses
A
$${\text{ionic character }}$$
B
$$\sigma {\text{ - character}}\,{\text{only}}$$
C
$$\pi {\text{ - character }}$$
D
$${\text{both}}\,\sigma \,{\text{and}}\,\pi \,{\text{characters}}$$
Answer :
$${\text{both}}\,\sigma \,{\text{and}}\,\pi \,{\text{characters}}$$
309. The correct name for the complex ion $${\left[ {CoCl\left( {ONO} \right){{\left( {en} \right)}_2}} \right]^ + }$$ is :
A
chlorobis ( ethylenediamine ) nitrito - $$O$$ - cobaltate (III) ion
B
chlorodiethyldiaminenitrito - $$O$$ - cobalt (III) ion
C
chloronitrito - $$O$$ - diethyldiamine cobaltate (III) ion
D
chlorobis ( ethylenediamine ) nitrito - $$O$$ - cobalt (III) ion
Answer :
chlorobis ( ethylenediamine ) nitrito - $$O$$ - cobalt (III) ion
310. Which of the following order of stability of complex ion is Incorrect?
A
$${\left[ {Fe{{\left( {{C_2}{O_4}} \right)}_3}} \right]^{3 - }} < {\left[ {Fe{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }}$$
B
$${\left[ {Fe\left( {edta} \right)} \right]^ - } > {\left[ {Fe{{\left( {en} \right)}_3}} \right]^{3 + }}$$
C
$${\left[ {Ni{{\left( {en} \right)}_2}} \right]^{2 + }} > \left[ {Ni{{\left( {dmg} \right)}_2}} \right]$$
D
$${\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{3 - }} > {\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{4 - }}$$
Answer :
$${\left[ {Ni{{\left( {en} \right)}_2}} \right]^{2 + }} > \left[ {Ni{{\left( {dmg} \right)}_2}} \right]$$
.PNG)
.PNG)