191. Which of the following ligands will not show chelation?
A
$$EDTA$$
B
$$DMG$$
C
$${\text{Ethane - 1, 2 - diamine}}$$
D
$$SC{N^ - }$$
Answer :
$$SC{N^ - }$$
192. Ammonia forms the complex ion $${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$ with copper ions in alkaline solutions but not in acidic solutions. What is the reason for it?
A
In acidic solutions protons coordinate with ammonia molecules forming $$NH_4^ + $$ ions and $$N{H_3}$$ molecules are not available
B
In alkaline solutions insoluble $$Cu{\left( {OH} \right)_2}$$ is precipitated which is soluble in excess of any alkali
C
Copper hydroxide is an amphoteric substance
D
In acidic solutions hydration protects copper ions
Answer :
In acidic solutions protons coordinate with ammonia molecules forming $$NH_4^ + $$ ions and $$N{H_3}$$ molecules are not available
193. Correct increasing order for the wavelengths of absorption in the visible region for the complexes of $$C{O^{3 + }}$$ is
A
$${\left[ {Co{{\left( {en} \right)}_3}} \right]^{3 + }},{\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }}$$
B
$${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {en} \right)}_3}} \right]^{3 + }},{\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }}$$
C
$${\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {en} \right)}_3}} \right]^{3 + }}$$
D
$${\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {en} \right)}_3}} \right]^{3 + }},{\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }}$$
Answer :
$${\left[ {Co{{\left( {en} \right)}_3}} \right]^{3 + }},{\left[ {Co{{\left( {N{H_3}} \right)}_6}} \right]^{3 + }},{\left[ {Co{{\left( {{H_2}O} \right)}_6}} \right]^{3 + }}$$
194. $$M{n^{2 + }}$$ forms a complex with $$B{r^ - }\,ion.$$ The magnetic moment of the complex is $$5.92\,B.M.$$ What would be the probable formula and geometry of the complex ?
A
$${\left[ {MnB{r_6}} \right]^{4 - }},{\text{octahedral}}$$
B
$${\left[ {MnB{r_4}} \right]^{2 - }},{\text{square planar}}$$
C
$${\left[ {MnB{r_4}} \right]^{2 - }},{\text{tetrahedral}}$$
D
$${\left[ {MnB{r_5}} \right]^{3 - }},{\text{trigonal bipyramidal}}$$
Answer :
$${\left[ {MnB{r_4}} \right]^{2 - }},{\text{tetrahedral}}$$
195. Pick out the correct statement with respect to $${\left[ {Mn{{\left( {CN} \right)}_6}} \right]^{3 - }}$$
A
It is $$s{p^3}{d^2}$$ hybridised and octahedral
B
It is $$s{p^3}{d^2}$$ hybridised and tetrahedral
C
It is $${d^2}s{p^3}$$ hybridised and octahedral
D
It is $$ds{p^2}$$ hybridised and square planar
Answer :
It is $${d^2}s{p^3}$$ hybridised and octahedral
196. The number of geometrical isomers for octahedral $${\left[ {Co{{\left( {N{H_3}} \right)}_2}C{l_4}} \right]^ - },$$ square planar $$AuC{l_2}Br_2^ - $$ and $${\left[ {Co\left( {N{O_2}} \right){{\left( {N{H_3}} \right)}_5}} \right]^{2 + }}$$ are
A
2, 2, 2
B
2, 2 , no isomerism
C
3, 2, 2
D
2, 3, no isomerism
Answer :
2, 2 , no isomerism
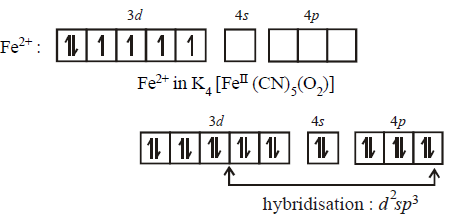
197. Which of the following statements is correct for the complex $$C{a_2}\left[ {Fe{{\left( {CN} \right)}_5}{O_2}} \right]$$ having $${t_{2g}}^6,{e_g}^0$$ electronic configuration ?
A
$${d^2}s{p^3}$$ hybridised and diamagnetic
B
$$s{p^3}{d^2}$$ hybridised and paramagnetic
C
$$s{p^3}{d^2}$$ hybridised and diamagnetic
D
$${d^2}s{p^3}$$ hybridised and paramagnetic
Answer :
$${d^2}s{p^3}$$ hybridised and paramagnetic
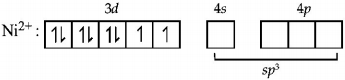
198. $$NiC{l_2}\,{\left\{ {P{{\left( {{C_2}{H_5}} \right)}_2}\left( {{C_6}{H_5}} \right)} \right\}_2}$$ exhibits temperature depend-ent magnetic behaviour (paramagnetic/diamagnetic). The coordination geometries of $$N{i^{2 + }}$$ in the paramagnetic and diamagnetic states are respectively.
A
tetrahedral and tetrahedral
B
square planar and square planar
C
tetrahedral and square planar
D
square planar and tetrahedral
Answer :
tetrahedral and square planar
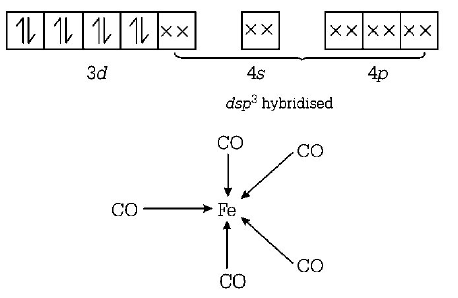
199. Shape of $$Fe{\left( {CO} \right)_5}$$ is
A
octahedral
B
square planar
C
trigonal bipyramidal
D
square pyramidal
Answer :
trigonal bipyramidal
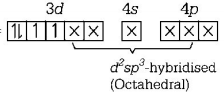
200. Which of the following statements related to crystal field splitting in octahedral coordination entities is incorrect ?
A
The $$d{x^2} - {y^2}$$ and $$d{z^2}$$ orbitals has more energy as compared to $${d_{xy}},{d_{yz}}$$ and $${d_{xz}}$$ orbitals.
B
Crystal field splitting energy $$\left( {{\Delta _ \circ }} \right)$$ depends directly on the charge of the metal ion and on the field produced by the ligand.
C
In the presence of $$B{r^ - }$$ as a ligand the distribution of electrons for $${d^4}$$ configuration will be $$t_{{2_g}}^3,e_g^1,$$
D
In the presence of $$C{N^ - }$$ as a ligand $${\Delta _ \circ } < P.$$
Answer :
In the presence of $$C{N^ - }$$ as a ligand $${\Delta _ \circ } < P.$$



.PNG)