131.
A ray of light is incident at the glass-water interface at an angle $$i,$$ it emerges finally parallel to the surface of water, then the value of $${\mu _g}$$ would be

A
$$\left( {\frac{4}{3}} \right)\sin i$$
B
$${\frac{1}{{\sin i}}}$$
C
$${\frac{4}{3}}$$
D
1
Answer :
$${\frac{1}{{\sin i}}}$$
132. Two lenses of power $$- 15\,D$$ and $$+ 5\,D$$ are in contact with each other. The focal length of the combination is
A
$$+ 10\,cm$$
B
$$- 20\,cm$$
C
$$- 10\,cm$$
D
$$+ 20\,cm$$
Answer :
$$- 10\,cm$$
133. The interference pattern is obtained with two coherent light sources of intensity ratio $$n.$$ In the interference pattern, the ratio $$\frac{{{I_{\max }} - {I_{\min }}}}{{{I_{\max }} + {I_{\min }}}}$$ will be
A
$$\frac{{\sqrt n }}{{n + 1}}$$
B
$$\frac{{2\sqrt n }}{{n + 1}}$$
C
$$\frac{{\sqrt n }}{{{{\left( {n + 1} \right)}^2}}}$$
D
$$\frac{{2\sqrt n }}{{{{\left( {n + 1} \right)}^2}}}$$
Answer :
$$\frac{{2\sqrt n }}{{n + 1}}$$
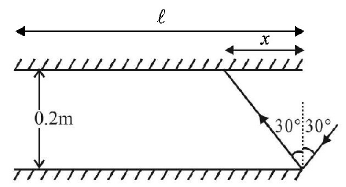
134.
Two plane mirrors $$A$$ and $$B$$ are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle 30° at a point just inside one end of $$A.$$ The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (including the first one) before it emerges out is
A
28
B
30
C
32
D
34
Answer :
30
135. An astronomical telescope has a large aperture to
A
reduce spherical aberration
B
have high resolution
C
increase span of observation
D
have low dispersion.
Answer :
have high resolution
136. The refracting angle of a prism is $$A,$$ and refractive index of the material of the prism is $$\cot \left( {\frac{A}{2}} \right).$$ The angle of minimum deviation is
A
$${180^ \circ } - 3A$$
B
$${180^ \circ } - 2A$$
C
$${90^ \circ } - A$$
D
$${180^ \circ } + 2A$$
Answer :
$${180^ \circ } - 2A$$
137.
A transparent solid cylindrical rod has a refractive index of $${\frac{2}{{\sqrt 3 }}}.$$ It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure.
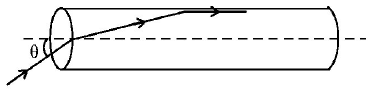
The incident angle $$\theta $$ for which the light ray grazes along the wall of the rod is:
A
$${\sin ^{ - 1}}\left( {\frac{{\sqrt 3 }}{2}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{2}{{\sqrt 3 }}} \right)$$
C
$${\sin ^{ - 1}}\left( {\frac{1}{{\sqrt 3 }}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{1}{{2}}} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\frac{1}{{\sqrt 3 }}} \right)$$
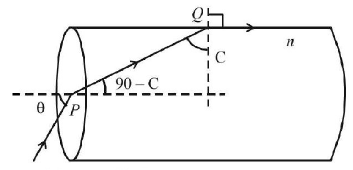
138.
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
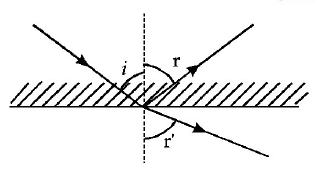
A
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
B
$${\sin ^{ - 1}}\left( {\tan i} \right)$$
C
$${\sin ^{ - 1}}\left( {\tan r'} \right)$$
D
$${\tan ^{ - 1}}\left( {\sin i} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
139. Light travels through a glass plate of thickness $$t$$ and refractive index $$\mu .$$ If $$c$$ is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
A
$$\mu tc$$
B
$$\frac{{tc}}{\mu }$$
C
$$\frac{1}{{\mu t}}$$
D
$$\frac{{\mu t}}{c}$$
Answer :
$$\frac{{\mu t}}{c}$$
140. When a ray of light enters a glass slab from air,
A
its wavelength decreases.
B
its wavelength increases.
C
Its frequency decreases.
D
neither its wavelength nor its frequency changes.
Answer :
its wavelength decreases.