71. The magnetic flux $$\phi $$ linked with a conducting coil depends on time as $$\phi = 4{t^n} + 6,$$ where $$n$$ is a positive constant. The induced emf in the coil is $$e.$$ Then which is wrong?
A
If $$0 < n < 1,\,e \ne 0$$ and $$\left| e \right|$$ decreases with time
B
If $$n = 1,$$ $$e$$ is constant
C
If $$n > 1,\left| e \right|$$ increases with time
D
If $$n > 1,\left| e \right|$$ decreases with time
Answer :
If $$n > 1,\left| e \right|$$ decreases with time
72. In a uniform magnetic field of induction $$B$$ a wire in the form of a semicircle of radius $$r$$ rotates about the diameter of the circle with an angular frequency $$\omega .$$ The axis of rotation is perpendicular to the field. If the total resistance of the circuit is $$R,$$ the mean power generated per period of rotation is
A
$$\frac{{{{\left( {B\pi r\omega } \right)}^2}}}{{2R}}$$
B
$$\frac{{{{\left( {B\pi {r^2}\omega } \right)}^2}}}{{8R}}$$
C
$$\frac{{B\pi {r^2}\omega }}{{2R}}$$
D
$$\frac{{{{\left( {B\pi r{\omega ^2}} \right)}^2}}}{{8R}}$$
Answer :
$$\frac{{{{\left( {B\pi {r^2}\omega } \right)}^2}}}{{8R}}$$
73. A superconducting loop of radius $$R$$ has self inductance $$L.$$ A uniform and constant magnetic field $$B$$ is applied perpendicular to the plane of the loop. Initially current in this loop is zero. The loop is rotated by $${180^ \circ }.$$ The current in the loop after rotation is equal to
A
zero
B
$$\frac{{B\pi {R^2}}}{L}$$
C
$$\frac{{2B\pi {R^2}}}{L}$$
D
$$\frac{{B\pi {R^2}}}{2L}$$
Answer :
$$\frac{{2B\pi {R^2}}}{L}$$
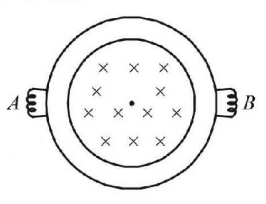
74.
A resistance less ring has 2 bulbs $$A$$ and $$B$$ rated at $$2V,10\,W$$ and $$2V,20\,W$$ respectively. The ring encloses an ideal solenoid whose magnetic field is as shown. The radius of solenoid is $$1\,m$$ and the number of $$\frac{{{\text{turns}}}}{{{\text{length}}}} = 1000/m.$$ The current changes at rate of $$9\,A/\sec.$$ Find the value of $$P$$ if power dissipated in bulb $$B$$ is $$1.8\,P \times {10^{ - 4}}\,watt.$$
A
4
B
6
C
8
D
11
Answer :
4
75.
There are three wire $$MO,NO$$ and $$PQ,$$ wires $$MO$$ and $$NO$$ are fixed and perpendicular to each other. Wire $$PQ$$ moves with a constant velocity $$v$$ as shown in the figure and resistance per unit length of each wire is $$\lambda $$ and magnetic field exists perpendicular and inside the paper then Which of the following is wrong?
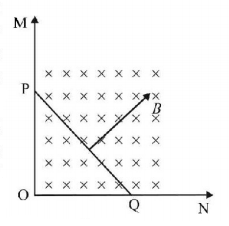
A
current in loop is anticlockwise
B
magnitude of current in the loop is $$\frac{{Bv}}{{\lambda \left( {\sqrt 2 + 1} \right)}}$$
C
current in the loop is independent of time.
D
magnitude of current decreases as time increases.
Answer :
magnitude of current decreases as time increases.
76.
Magnetic flux linked with a stationary loop of resistance $$R$$ varies with respect to time during the time period $$T$$ as follows:
$$\phi = at\left( {T - t} \right)$$
The amount of heat generated in the loop during that time (inductance of the coil is negligible) is
A
$$\frac{{aT}}{{3R}}$$
B
$$\frac{{{a^2}{T^2}}}{{3R}}$$
C
$$\frac{{{a^2}{T^2}}}{R}$$
D
$$\frac{{{a^2}{T^3}}}{{3R}}$$
Answer :
$$\frac{{{a^2}{T^3}}}{{3R}}$$
77.
In the figure the flux through the loop perpendicular to the plane of the coil and directed into the paper is varying according to the relation $$\phi = 6{t^2} + 7t + 1$$ where $$\phi $$ is in milliweber and $$t$$ is in second. The magnitude of the emf induced in the loop at $$t = 2\,s$$ and the direction of induce current through $$R$$ are
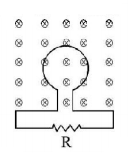
A
$$39\,mV;$$ right to left
B
$$39\,mV;$$ left to right
C
$$31\,mV;$$ right to left
D
$$31\,mV;$$ left to right
Answer :
$$39\,mV;$$ right to left
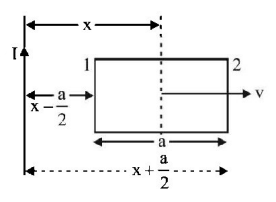
78.
A conducting square frame of side $$'a'$$ and a long straight wire carrying current $$I$$ are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity $$'V'.$$ The emf induced in the frame will be proportional to
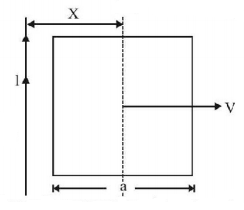
A
$$\frac{1}{{{{\left( {2x - a} \right)}^2}}}$$
B
$$\frac{1}{{{{\left( {2x + a} \right)}^2}}}$$
C
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
D
$$\frac{1}{{{x^2}}}$$
Answer :
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
79.
A coil of resistance $$400\,\Omega $$ is placed in a magnetic field. If the magnetic flux $$\phi \left( {Wb} \right)$$ linked with the coil varies with time $$t$$ (second) as $$\phi = 50\,{t^2} + 4.$$
The current in the coil at $$t = 2\,s$$ is
A
$$0.5\,A$$
B
$$0.1\,A$$
C
$$2\,A$$
D
$$1\,A$$
Answer :
$$0.5\,A$$
80.
Shown in the figure is a circular loop of radius $$r$$ and resistance $$R.$$ A variable magnetic field of induction $$B = {B_0}{e^{ - t}}$$ is established inside the coil. If the key $$\left( K \right)$$ is closed, the electrical power developed right after closing the switch is equal to
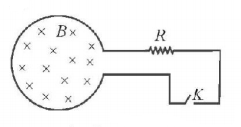
A
$$\frac{{B_0^2\pi {r^2}}}{R}$$
B
$$\frac{{{B_0}10{r^3}}}{R}$$
C
$$\frac{{B_0^2{\pi ^2}{r^4}R}}{5}$$
D
$$\frac{{B_0^2{\pi ^2}{r^4}}}{R}$$
Answer :
$$\frac{{B_0^2{\pi ^2}{r^4}}}{R}$$