61. A generator has an e.m.f. of $$440$$ Volt and internal resistance of $$4000\,hm.$$ Its terminals are connected to a load of $$4000\,ohm.$$ The voltage across the load is
A
220 volt
B
440 volt
C
200 volt
D
400 volt
Answer :
400 volt
62. What is the self-inductance of a coil which produces $$5V$$ when the current changes from $$3$$ ampere to $$2$$ ampere in one millisecond?
A
5000 henry
B
5 milli-henry
C
50 henry
D
5 henry
Answer :
5 milli-henry
63.
Two different wire loops are concentric and lie in the same plane. The current in the outer loop $$\left( I \right)$$ is clockwise and increases with time. The induced current in the inner loop
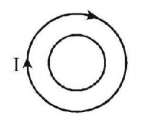
A
is clockwise
B
is zero
C
is counter clockwise
D
has a direction that depends on the ratio of the loop radii.
Answer :
is counter clockwise
64. Two identical cycle wheels (geometrically) have different number of spokes connected from center to rim. One is having 20 spokes and the other having only 10 (the rim and the spokes are resistanceless). One resistance of value $$R$$ is connected between center and rim. The current in $$R$$ will be
A
double in the first wheel than in the second wheel
B
four times in the first wheel than in the second wheel
C
will be double in the second wheel than that of the first wheel
D
will be equal in both these wheels
Answer :
will be equal in both these wheels
65. A conducting circular loop is placed in a uniform magnetic field $$0.04\,T$$ with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at $$2\,mm\,{s^{ - 1}}.$$ The induced emf in the loop when the radius is $$2\,cm$$ is
A
$$3.2\,\pi \mu V$$
B
$$4.8\,\pi \mu V$$
C
$$0.8\,\pi \mu V$$
D
$$1.6\,\pi \mu V$$
Answer :
$$3.2\,\pi \mu V$$
66. A varying current in a coil changes from $$10A$$ to zero in $$0.5\,\sec.$$ If the average e.m.f induced in the coil is $$220V,$$ the self-inductance of the coil is
A
$$5\,H$$
B
$$6\,H$$
C
$$11\,H$$
D
$$12\,H$$
Answer :
$$11\,H$$
67. A conducting circular loop made of a thin wire, has area $$3.5 \times {10^{ - 3}}{m^{ - 2}}$$ and resistance 10$$\Omega $$. It is placed perpendicular to a time dependent magnetic field $$B\left( t \right) = \left( {0.4T} \right)\sin \left( {50\pi t} \right).$$ The the net charge flowing through the loop during $$t= 0\,s$$ and $$t = 10\,ms$$ is close to:
A
$$0.14\,mC$$
B
$$7\,mC$$
C
$$0.21\,mC$$
D
$$6\,mC$$
Answer :
$$0.14\,mC$$
68. A metal conductor of length $$1m$$ rotates vertically about one of its ends at angular velocity 5 radians per second. If the horizontal component of earth’s magnetic field is $$0.2 \times {10^{ - 4}}T,$$ then the e.m.f. developed between the two ends of the conductor is
A
$$5mV$$
B
$$50\,\mu V$$
C
$$5\,\mu V$$
D
$$50mV$$
Answer :
$$50\,\mu V$$
69. A motor having an armature of resistance $$2\Omega $$ is designed to operate at $$220\,V$$ mains. At full speed, it develops a back emf of $$210V.$$ When the motor is running at full speed, the current in the armature is:
A
$$3\,A$$
B
$$5\,A$$
C
$$7\,A$$
D
$$10\,A$$
Answer :
$$5\,A$$
70. A conducting square loop is placed in a magnetic field $$B$$ with its plane perpendicular to the field. The sides of the loop start shrinking at a constant rate $$\alpha .$$ The induced emf in the loop at an instant when its side is $$'a'$$ is
A
$$2a\alpha B$$
B
$${a^2}\alpha B$$
C
$$2{a^2}\alpha B$$
D
$$a\alpha B$$
Answer :
$$2a\alpha B$$