21. A long solenoid of diameter $$0.1\,m$$ has $$2 \times {10^4}$$ turns per metre. At the centre of the solenoid, a coil of 100 turns and radius $$0.01\,m$$ is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to $$0\,A$$ from $$4\,A$$ in $$0.05\,s.$$ If the resistance of the coil is $$10\,{\pi ^2}\Omega ,$$ the total charge flowing through the coil during this time is
A
$$32\,\pi \mu C$$
B
$$16\,\mu C$$
C
$$32\,\mu C$$
D
$$16\,\pi \mu C$$
Answer :
$$32\,\mu C$$
22.
The figure shows certain wire segments joined together to form a coplanar loop. The loop is placed in a perpendicular magnetic field in the direction going into the plane of the figure. The magnitude of the field increases with time. $${I_1}$$ and $${I_2}$$ are the currents in the segments $$ab$$ and $$cd.$$ Then,

A
$${I_1} > {I_2}$$
B
$${I_1} < {I_2}$$
C
$${I_1}$$ is in the direction $$ba$$ and $${I_2}$$ is in the direction $$cd$$
D
$${I_1}$$ is in the direction $$ab$$ and $${I_2}$$ is in the direction $$dc$$
Answer :
$${I_1}$$ is in the direction $$ab$$ and $${I_2}$$ is in the direction $$dc$$
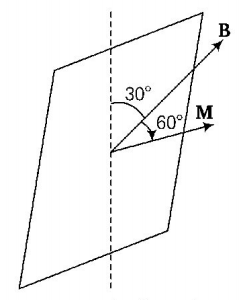
23. A circular disc of radius $$0.2\,m$$ is placed in a uniform magnetic field of induction $$\frac{1}{\pi }\left( {Wb/{m^2}} \right)$$ in such a way that its axis makes an angle of $${60^ \circ }$$ with $$B.$$ The magnetic flux linked with the disc is
A
$$0.02\,Wb$$
B
$$0.06\,Wb$$
C
$$0.08\,Wb$$
D
$$0.01\,Wb$$
Answer :
$$0.02\,Wb$$
24. A nonconducting ring of mass $$m$$ and radius $$R$$ has a charge $$Q$$ uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field $$B = {B_0}{t^2}$$ tesla is switched on. After $$2$$ second from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre. Then
A
the induced electric field is quadratic in time $$t$$
B
the force tangential to the ring is $$9{B_0}QRt$$
C
until $$2$$ seconds, the friction force does not come into play
D
the friction coefficient between the ring and the surface is $$\frac{{2{B_0}RQ}}{{mg}}$$
Answer :
the friction coefficient between the ring and the surface is $$\frac{{2{B_0}RQ}}{{mg}}$$
25. In an oscillating $$LC$$ circuit the maximum charge on the capacitor is $$Q.$$ The charge on the capacitor when the energy is stored equally between the electric and magnetic field is
A
$$\frac{Q}{2}$$
B
$$\frac{Q}{{\sqrt 3 }}$$
C
$$\frac{Q}{{\sqrt 2 }}$$
D
$$Q$$
Answer :
$$\frac{Q}{{\sqrt 2 }}$$
26. A circular coil is radius $$5\,cm$$ has $$500$$ turns of a wire. The approximate value of the coefficient of self induction of the coil will be-
A
$$25\,mH$$
B
$$25 \times {10^{ - 3}}mH$$
C
$$50 \times {10^{ - 3}}mH$$
D
$$50 \times {10^{ - 3}}H$$
Answer :
$$25\,mH$$
27.
A square metal wire loop of side $$10\,cm$$ and resistance 1 ohm is moved with a constant velocity $${v_0}$$ in a uniform magnetic field of induction $$B = 2\,{\text{weber}}/{m^2}$$ as shown in the figure. The magnetic field lines are perpendicular to the plane of the loop (directed into the paper). The loop is connected to a network of resistors each of value 3 ohms. The resistances of the lead wires $$OS$$ and $$PQ$$ are negligible. What should be the speed of the loop so as to have a steady current of 1 milliampere in the loop ? Give the direction of current in the loop.
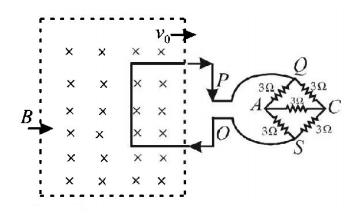
A
$$2.3\,m/s$$
B
$$1.2\,m/s$$
C
$$0.3\,m/s$$
D
$$0.02\,m/s$$
Answer :
$$0.02\,m/s$$
28. When a metallic plate swings between the poles of a magnet
A
no effect on the plate
B
eddy currents are set up inside the plate and the direction of the current is along the motion of the plate
C
eddy currents are set up inside the plate and the direction of the current opposes the motion of the plate
D
eddy currents are set up inside the plate
Answer :
eddy currents are set up inside the plate and the direction of the current opposes the motion of the plate
29.
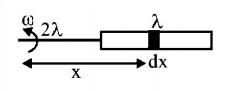
A metallic rod of length $$'\ell '$$ is tied to a string of length $$2\ell $$ and made to rotate with angular speed $$\omega $$ on a horizontal table with one end of the string fixed. If there is a vertical magnetic field $$'B'$$ in the region, the e.m.f. induced across the ends of the rod is
A
$$\frac{{2B\omega {\ell ^2}}}{2}$$
B
$$\frac{{3B\omega {\ell ^2}}}{2}$$
C
$$\frac{{4B\omega {\ell ^2}}}{2}$$
D
$$\frac{{5B\omega {\ell ^2}}}{2}$$
Answer :
$$\frac{{5B\omega {\ell ^2}}}{2}$$
30. A rectangular coil of length $$0.12\,m$$ and width $$0.1\,m$$ having 50 turns of wire is suspended vertically in a uniform magnetic field of strength $$0.2\,Wb/{m^2}.$$ The coil carries a current of $$2\,A.$$ If the plane of the coil is inclined at an angle of $${30^ \circ }$$ with the direction of the field, the torque required to keep the coil in stable equilibrium will be
A
$$0.15\,Nm$$
B
$$0.20\,Nm$$
C
$$0.24\,Nm$$
D
$$0.12\,Nm$$
Answer :
$$0.20\,Nm$$