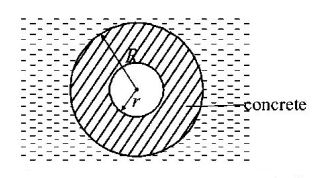
181. A concrete sphere of radius $$R$$ has a cavity of radius $$r$$ which is packed with sawdust. The specific gravities of concrete and sawdust are respectively 2.4 and 0.3 for this sphere to float with its entire volume submerged under water. Ratio of mass of concrete to mass of sawdust will be
A
8
B
4
C
3
D
zero
Answer :
4
182. Two wires of equal lengths are made of the same material. Wire $$A$$ has a diameter that is twice as that of wire $$B.$$ If identical weights are suspended from the ends of these wires, the increase in length is
A
four times for wire $$A$$ as for wire $$B$$
B
twice for wire $$A$$ as for wire $$B$$
C
half for wire $$A$$ as for wire $$B$$
D
one-fourth for wire $$A$$ as for wire $$B$$
Answer :
one-fourth for wire $$A$$ as for wire $$B$$
183. A body of mass $$10\,kg$$ is attached to a wire of radius $$3\,cm.$$ It’s breaking stress is $$4.8 \times {10^7}\,N{m^{ - 2}},$$ the area of cross-section of the wire is $${10^{ - 6}}{m^2}.$$ What is the maximum angular velocity with which it can be rotated in the horizontal circle?
A
$$1\,rad\,{\sec ^{ - 1}}$$
B
$$2\,rad\,{\sec ^{ - 1}}$$
C
$$4\,rad\,{\sec ^{ - 1}}$$
D
$$8\,rad\,{\sec ^{ - 1}}$$
Answer :
$$4\,rad\,{\sec ^{ - 1}}$$
184. After terminal velocity is reached, the acceleration of a body falling through a fluid is
A
equal to $$g$$
B
zero
C
less than $$g$$
D
greater than $$g$$
Answer :
zero
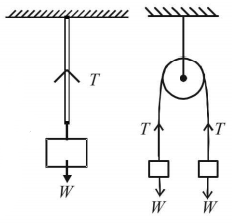
185. A wire elongates by $$l \,mm$$ when a load $$W$$ is hanged from it. If the wire goes over a pulley and two weights $$W$$ each are hung at the two ends, the elongation of the wire will be (in $$mm$$ )-
A
$$l$$
B
$$2l$$
C
$$zero$$
D
$$\frac{l}{2}$$
Answer :
$$l$$
186. A vertical capillary tube with inside diameter a $$0.5\,mm$$ is submerged into water so that the length of its part protruding over the surface of water is equal to $$2.5\,mm.$$ Find the radius of curvature of the meniscus.
A
$$0.3\,mm$$
B
$$0.6\,mm$$
C
$$0.9\,mm$$
D
$$1.2\,mm$$
Answer :
$$0.6\,mm$$
187. A certain number of spherical drops of a liquid of radius $$r$$ coalesce to form a single drop of radius $$R$$ and volume $$V.$$ If $$T$$ is the surface tension of the liquid, then
A
energy $$ = 4VT\left( {\frac{1}{r} - \frac{1}{R}} \right)$$ is released
B
energy $$ = 3VT\left( {\frac{1}{r} + \frac{1}{R}} \right)$$ is absorbed
C
energy $$ = 3VT\left( {\frac{1}{r} - \frac{1}{R}} \right)$$ is released
D
energy is neither released nor absorbed
Answer :
energy $$ = 3VT\left( {\frac{1}{r} - \frac{1}{R}} \right)$$ is released
188.
The lower end of a capillary tube of radius $$2.00\,mm$$ is dipped $$10.00\,cm$$ below the surface of water in a beaker. Calculate the pressure within a bubble blown at its end in water, in excess of atmospheric pressure.
[Surface tension of water $$72 \times {10^{ - 3}}\,N/m$$ ]
A
$$718\,N{m^{ - 2}}$$
B
$$912\,N{m^{ - 2}}$$
C
$$1160\,N{m^{ - 2}}$$
D
$$1052\,N{m^{ - 2}}$$
Answer :
$$1052\,N{m^{ - 2}}$$
189. As the temperature of a liquid is raised, the coefficient of viscosity
A
decreases
B
increases
C
remains the same
D
may increase or decrease depending on the nature of liquid
Answer :
decreases
190. A wide vessel with a small hole at the bottom is filled with water (density $${\rho _1},$$ height $${h_1}$$) and kerosene (density $${\rho _2},$$ height $${h_2}$$ ). Neglecting viscosity effects, the speed with which water flows out is :
A
$${\left[ {2g\left( {{h_1} + {h_2}} \right)} \right]^{\frac{1}{2}}}$$
B
$${\left[ {2g\left( {{h_1}{\rho _1} + {h_2}{\rho _2}} \right)} \right]^{\frac{1}{2}}}$$
C
$${\left[ {2g\left( {{h_1} + {h_2}\left( {\frac{{{\rho _2}}}{{{\rho _1}}}} \right)} \right)} \right]^{\frac{1}{2}}}$$
D
$${\left[ {2g\left( {{h_1} + {h_2}\left( {\frac{{{\rho _1}}}{{{\rho _2}}}} \right)} \right)} \right]^{\frac{1}{2}}}$$
Answer :
$${\left[ {2g\left( {{h_1} + {h_2}\left( {\frac{{{\rho _2}}}{{{\rho _1}}}} \right)} \right)} \right]^{\frac{1}{2}}}$$