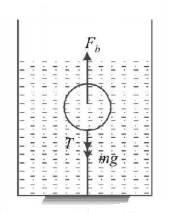
171. The total weight of a piece of wood is $$6\,kg.$$ In the floating state in water its $$\frac{1}{3}$$ part remains inside the water. On this floating piece of wood what maximum weight is to be put such that the whole of the piece of wood is to be drowned in the water?
A
$$15\,kg$$
B
$$14\,kg$$
C
$$10\,kg$$
D
$$12\,kg$$
Answer :
$$12\,kg$$
172.
When the load on a wire is increasing slowly from $$2\,kg$$ to $$4\,kg,$$ the elongation increases from $$0.6\,mm$$ to $$1\,mm.$$ The work done during this extension of the wire is
$$\left( {g = 10\,m/{s^2}} \right)$$
A
$$9 \times {10^{ - 3}}J$$
B
$$12 \times {10^{ - 3}}J$$
C
$$14 \times {10^{ - 3}}J$$
D
$$16 \times {10^{ - 3}}J$$
Answer :
$$14 \times {10^{ - 3}}J$$
173.
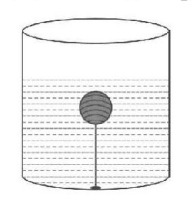
A solid sphere of density $$\eta \left( { > 1} \right)$$ times lighter than water is suspended in a water tank by a string tied to its base as shown in fig. If the mass of the sphere is $$m,$$ then the tension in the string is given by
A
$$\left( {\frac{{\eta - 1}}{\eta }} \right)mg$$
B
$$\eta mg$$
C
$$\frac{{mg}}{{\eta - 1}}$$
D
$$\left( {\eta - 1} \right)mg$$
Answer :
$$\left( {\eta - 1} \right)mg$$
174. Two, spring $$P$$ and $$Q$$ of force constants $${k_p}$$ and $${k_Q}\left( {{k_Q} = \frac{{{k_p}}}{2}} \right)$$ are stretched by applying forces of equal magnitude. If the energy stored in $$Q$$ is $$E,$$ then the energy stored in $$P$$ is
A
$$E$$
B
$$2E$$
C
$$\frac{E}{2}$$
D
$$\frac{E}{4}$$
Answer :
$$\frac{E}{2}$$
175. The following four wires are made of same material. Which of these will have the largest extension when the same tension is applied?
A
Length $$= 50\,cm,$$ diameter $$= 0.5\,mm$$
B
Length $$= 100\,cm,$$ diameter $$= 1\,mm$$
C
Length $$= 200\,cm,$$ diameter $$= 2\,mm$$
D
Length $$= 300\,cm,$$ diameter $$= 3\,mm$$
Answer :
Length $$= 50\,cm,$$ diameter $$= 0.5\,mm$$
176. If $$'S\,'$$ is stress and $$'Y\,'$$ is young’s modulus of material of a wire, the energy stored in the wire per unit volume is-
A
$$\frac{{{S^2}}}{{2Y}}$$
B
$$2{S^2}Y$$
C
$$\frac{S}{{2Y}}$$
D
$$\frac{{2Y}}{{{S^2}}}$$
Answer :
$$\frac{{{S^2}}}{{2Y}}$$
177. Two wires are made of the same material and have the same volume. However first wire has cross-sectional area $$A$$ and second wire has cross-sectional area $$5A.$$ If the length of first wire increases by $$\Delta l$$ on applying force $$f,$$ how much force is needed to stretch second wire by the same amount?
A
$$14f$$
B
$$6f$$
C
$$25f$$
D
$$9f$$
Answer :
$$9f$$
178.
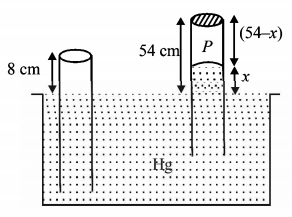
An open glass tube is immersed in mercury in such a way that a length of $$8 \,cm$$ extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional $$46 \,cm.$$ What will be length of the air column above mercury in the tube now?
(Atmospheric pressure $$= 76 \,cm$$ of $$Hg$$ )
A
$$16\,cm$$
B
$$22\,cm$$
C
$$38\,cm$$
D
$$6\,cm$$
Answer :
$$16\,cm$$
179.
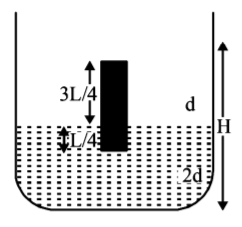
A homogeneous solid cylinder of length $$L\left( {L < \frac{H}{2}} \right),$$ cross-sectional area $$\frac{A}{5}$$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $$\frac{L}{4}$$ in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure $${P_0}.$$ Then density $$D$$ of solid is given by-
A
$$\frac{5}{4}d$$
B
$$\frac{4}{5}d$$
C
$$4d$$
D
$$\frac{d}{5}$$
Answer :
$$\frac{5}{4}d$$
180. The Young's modulus of the material of a wire is $$2 \times {10^{10}}N{m^{ - 2}}.$$ If the elongation strain is $$1\% ,$$ then the energy stored in the wire per unit volume in $$J{m^{ - 3}}$$ is
A
$${10^{6}}$$
B
$${10^{8}}$$
C
$$2 \times {10^6}$$
D
$$2 \times {10^8}$$
Answer :
$${10^{6}}$$