151.
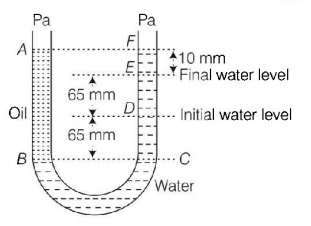
A $$U$$ tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of $$10\,mm$$ above the water level on the other side. Meanwhile the water rises by $$65\,mm$$ from its original level (see diagram). The density of the oil is
A
$$650\,kg\,{m^{ - 3}}$$
B
$$425\,kg\,{m^{ - 3}}$$
C
$$800\,kg\,{m^{ - 3}}$$
D
$$928\,kg\,{m^{ - 3}}$$
Answer :
$$928\,kg\,{m^{ - 3}}$$
152. Water is flowing on a horizontal fixed surface, such that its flow velocity varies with $$y$$ (vertical direction) as $$v = k\left( {\frac{{2{y^2}}}{{{a^2}}} - \frac{{{y^3}}}{{{a^3}}}} \right).$$ If coefficient of viscosity for water is $$\eta ,$$ what will be shear stress between layers of water at $$y = a.$$
A
$$\frac{{\eta k}}{a}$$
B
$$\frac{\eta }{{ka}}$$
C
$$\frac{{\eta a}}{k}$$
D
None of these
Answer :
$$\frac{{\eta k}}{a}$$
153. A spring of force constant $$800 \,N/m$$ has an extension of $$5 \,cm.$$ The work done in extending it from $$5 \,cm$$ to $$15 \,cm$$ is-
A
$$16\,J$$
B
$$8\,J$$
C
$$32\,J$$
D
$$24\,J$$
Answer :
$$8\,J$$
154. A $$5$$ metre long wire is fixed to the ceiling. A weight of $$10\,kg$$ is hung at the lower end and is $$1$$ metre above the floor. The wire was elongated by $$1\,mm.$$ The energy stored in the wire due to stretching is
A
zero
B
0.05 joule
C
100 joule
D
500 joule
Answer :
0.05 joule
155. A metal wire of length $${L_1}$$ and area of cross-section $$A$$ is attached to a rigid support. Another metal wire of length $${L_2}$$ and of the same cross-sectional area is attached to the free end of the first wire. A body of mass $$M$$ is then suspended from the free end of the second wire. If $${Y_1}$$ and $${Y_2}$$ are the young’s moduli of the wires respectively, the effective force constant of the system of two wires is
A
$$\frac{{\left( {{Y_1}{Y_2}} \right)A}}{{2\left( {{Y_1}{L_2} + {Y_2}{L_1}} \right)}}$$
B
$$\frac{{\left( {{Y_1}{Y_2}} \right)A}}{{{{\left( {{L_1}{L_2}} \right)}^{\frac{1}{2}}}}}$$
C
$$\frac{{\left( {{Y_1}{Y_2}} \right)A}}{{{Y_1}{L_2} + {Y_2}{L_1}}}$$
D
$$\frac{{{{\left( {{Y_1}{Y_2}} \right)}^{\frac{1}{2}}}A}}{{{{\left( {{L_2}{L_1}} \right)}^{\frac{1}{2}}}}}$$
Answer :
$$\frac{{\left( {{Y_1}{Y_2}} \right)A}}{{{Y_1}{L_2} + {Y_2}{L_1}}}$$
156. Spherical balls of radius $$'R\,'$$ are falling in a viscous fluid of viscosity $$'\eta \,'$$ with a velocity $$'v\,'.$$ The retarding viscous force acting on the spherical ball is-
A
inversely proportional to both radius $$'R\,'$$ and velocity $$'v\,'$$
B
directly proportional to both radius $$'R\,'$$ and velocity $$'v\,'$$
C
directly proportional to $$'R\,'$$ but inversely proportional to $$'v\,'$$
D
inversely proportional to $$'R\,'$$ but directly proportional to velocity $$'v\,'$$
Answer :
directly proportional to both radius $$'R\,'$$ and velocity $$'v\,'$$
157. The two thigh bones, each of cross-sectional area $$10\,c{m^2}$$ support the upper part of a human body of mass $$40\,kg.$$ Estimate the average pressure sustained by the bones. Take $$g = 10\,m/{s^2}$$
A
$$2 \times {10^5}\,N/{m^2}$$
B
$$5 \times {10^4}\,N/{m^2}$$
C
$$2 \times {10^7}\,N/{m^2}$$
D
$$3 \times {10^6}\,N/{m^2}$$
Answer :
$$2 \times {10^5}\,N/{m^2}$$
158. The average mass of rain drops is $$3.0 \times {10^{ - 5}}kg$$ and their average terminal velocity is $$9\,m/s.$$ Calculate the energy transferred by rain to each square metre of the surface at a place which receives $$100\,cm$$ of rain in a year.
A
$$3.5 \times {10^5}\,J$$
B
$$4.05 \times {10^4}\,J$$
C
$$3.0 \times {10^5}\,J$$
D
$$9.0 \times {10^4}\,J$$
Answer :
$$4.05 \times {10^4}\,J$$
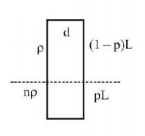
159. Two non-mixing liquids of densities $$\rho $$ and $$n\rho \left( {n > 1} \right)$$ are put in a container. The height of each liquid is $$h.$$ A solid cylinder of length $$L$$ and density $$d$$ is put in this container. The cylinder floats with its axis vertical and length $$pL\left( {p < 1} \right)$$ in the denser liquid. The density $$d$$ is equal to:
A
$$\left\{ {1 + \left( {n + 1} \right)p} \right\}\rho $$
B
$$\left\{ {2 + \left( {n + 1} \right)p} \right\}\rho $$
C
$$\left\{ {2 + \left( {n - 1} \right)p} \right\}\rho $$
D
$$\left\{ {1 + \left( {n - 1} \right)p} \right\}\rho $$
Answer :
$$\left\{ {1 + \left( {n - 1} \right)p} \right\}\rho $$
160. If $$'M\,'$$ is the mass of water that rises in a capillary tube of radius $$'r\,',$$ then mass of water which will rise in a capillary tube of radius $$'2\,r\,'$$ is-
A
$$M$$
B
$$\frac{M}{2}$$
C
$$4\,M$$
D
$$2\,M$$
Answer :
$$2\,M$$