131. The following four wires are made of the same material, Which of these will have the largest extension when the same tension is applied ?
A
length $$= 50\,cm,$$ diameter $$= 0.5\,mm$$
B
length $$= 100\,cm,$$ diameter $$= 1\,mm$$
C
length $$= 200\,cm,$$ diameter $$= 2\,mm$$
D
length $$= 300\,cm,$$ diameter $$= 3\,mm.$$
Answer :
length $$= 50\,cm,$$ diameter $$= 0.5\,mm$$
132. A force of $${10^3}$$ newton, stretches the length of a hanging wire by $$1$$ millimetre. The force required to stretch a wire of same material and length but having four times the diameter by $$1$$ millimetre is
A
$$4 \times {10^3}N$$
B
$$16 \times {10^3}N$$
C
$$\frac{1}{4} \times {10^3}N$$
D
$$\frac{1}{{16}} \times {10^3}N$$
Answer :
$$16 \times {10^3}N$$
133. The molecules of a given mass of a gas have $$r.m.s.$$ velocity of $$200\,m{s^{ - 1}}$$ at $${27^ \circ }C$$ and $$1.0 \times {10^5}N{m^{ - 2}}$$ pressure. When the temperature and pressure of the gas are respectively, $${127^ \circ }C$$ and $$0.05 \times {10^5}N{m^{ - 2}},$$ the $$rms$$ velocity of its molecules in $$m{s^{ - 1}}$$ is
A
$$\frac{{400}}{{\sqrt 3 }}$$
B
$$\frac{{100\sqrt 2 }}{3}$$
C
$$\frac{{100}}{3}$$
D
$$100\sqrt 2 $$
Answer :
$$\frac{{400}}{{\sqrt 3 }}$$
134.
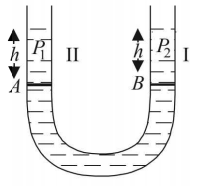
A U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by $$2 \,cm.$$ If the specific gravity of liquid I is $$1.1,$$ the specific gravity of liquid II must be-
A
$$1.12$$
B
$$1.1$$
C
$$1.05$$
D
$$1.0$$
Answer :
$$1.1$$
135.
Two cylinders $$A$$ and $$B$$ of the same material have same length, their radii being in the ratio $$1 : 2$$ respectively. The two are joined end to end as shown. One end of cylinder $$A$$ is rigidly clamped while free end of cylinder $$B$$ is twisted through an angle $$\theta .$$ The angle of twist of cylinder $$A$$ is

A
$$\frac{{16}}{{17}}\theta $$
B
$$\frac{{15}}{{16}}\theta $$
C
$$8\theta $$
D
$$\frac{3}{2}\theta $$
Answer :
$$\frac{{16}}{{17}}\theta $$
136. A material has poisson's ratio $$0.50.$$ If a uniform rod of it suffers a longitudinal strain of $$2 \times {10^{ - 3}},$$ then the percentage change in volume is
A
0.6
B
0.4
C
0.2
D
Zero
Answer :
0.4
137. A spherical solid ball of volume $$V$$ is made of a material of density $${\rho _1}.$$ It is falling through a liquid of density $${\rho _2}\left( {{\rho _2} < {\rho _1}} \right).$$ Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $$v,$$ i.e., $${F_{viscous}} = - k{v^2}\left( {k > 0} \right).$$ The terminal speed of the ball is-
A
$$\sqrt {\frac{{Vg\left( {{\rho _1} - {\rho _2}} \right)}}{k}} $$
B
$$\frac{{Vg{\rho _1}}}{k}$$
C
$$\sqrt {\frac{{Vg{\rho _1}}}{k}} $$
D
$${\frac{{Vg\left( {{\rho _1} - {\rho _2}} \right)}}{k}}$$
Answer :
$$\sqrt {\frac{{Vg\left( {{\rho _1} - {\rho _2}} \right)}}{k}} $$
138. A balloon of volume $$V,$$ contains a gas whose density is to that of the air at the earth’s surface as $$1:15.$$ If the envelope of the balloon be of weight $$w$$ but of negligible volume, find the acceleration with which it will begin to ascend.
A
$$\left( {\frac{{7Vg\sigma - w}}{{Vg\sigma + w}}} \right) \times g$$
B
$$\left( {\frac{{2Vg\sigma - w}}{{Vg\sigma + w}}} \right) \times g$$
C
$$\left( {\frac{{14Vg\sigma - w}}{{Vg\sigma + w}}} \right) \times g$$
D
$$\left( {\frac{{14Vg\sigma + w}}{{Vg\sigma - w}}} \right) \times g$$
Answer :
$$\left( {\frac{{14Vg\sigma - w}}{{Vg\sigma + w}}} \right) \times g$$
139. The bulk modulus of a spherical object is $$B.$$ If it is subjected to uniform pressure $$p,$$ the fractional decrease in radius is
A
$$\frac{p}{B}$$
B
$$\frac{B}{{3p}}$$
C
$$\frac{{3p}}{B}$$
D
$$\frac{p}{{3B}}$$
Answer :
$$\frac{p}{{3B}}$$
140. A $$20 \,cm$$ long capillary tube is dipped in water. The water rises up to $$8 \,cm.$$ If the entire arrangement is put in a freely falling elevator the length of water column in the capillary tube will be-
A
$$10 \,cm$$
B
$$8 \,cm$$
C
$$20 \,cm$$
D
$$4 \,cm$$
Answer :
$$20 \,cm$$