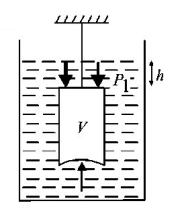
111.
A hemispherical portion of radius $$R$$ is removed from the bottom of a cylinder of radius $$R.$$ The volume of the remaining cylinder is $$V$$ and its mass $$M.$$ It is suspended by a string in a liquid of density $$\rho $$ where it stays vertical. The upper surface of the cylinder is at a depth $$h$$ below the liquid surface. The force on the bottom of the cylinder by the liquid is
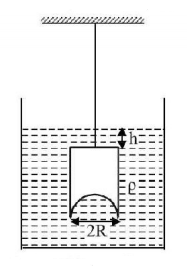
A
$$Mg$$
B
$$Mg - V\rho g$$
C
$$Mg + \pi {R^2}h\rho g$$
D
$$\rho g\left( {V + \pi {R^2}h} \right)$$
Answer :
$$\rho g\left( {V + \pi {R^2}h} \right)$$
112. Two persons pull a rope towards themselves. Each person exerts a force of $$100\,N$$ on the rope. Find the Young's modulus of the material of the rope if it extends in length by $$1\,cm.$$ Original length of the rope $$= 2\,m$$ and the area of cross-section $$ = 2\,c{m^2}.$$
A
$${10^8}\,N/{m^2}$$
B
$${10^7}\,N/{m^2}$$
C
$${10^6}\,N/{m^2}$$
D
$${10^5}\,N/{m^2}$$
Answer :
$${10^8}\,N/{m^2}$$
113. A ball is made of a material of density $$\rho $$ where $${\rho _{oil}} < \rho < {\rho _{water}}$$ with $${\rho _{oil}}$$ and $${\rho _{water}}$$ representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?
A
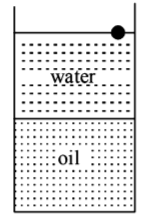

B
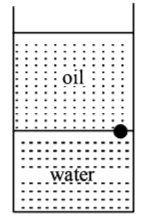

C
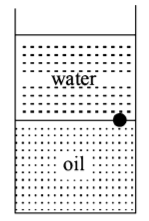

D
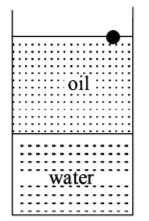

Answer :


114.
In a cylindrical water tank, there are two small holes $$A$$ and $$B$$ on the wall at a depth of $${h_1},$$ from the surface of water and at a height of $${h_2}$$ from the bottom of water tank. Surface of water is at height of $${h_2}$$ from the bottom of water tank. Surface of water is at height $$H$$ from the bottom of water tank. Water coming out from both holes strikes the ground at the same point $$S.$$ Find the ratio of $${h_1}$$ and $${h_2}$$
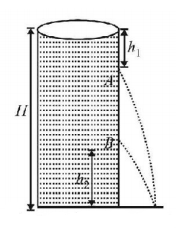
A
Depends on $$H$$
B
$$1:1$$
C
$$2:2$$
D
$$1:2$$
Answer :
$$1:1$$
115. A solid cube is subjected to a pressure of $$5 \times {10^5}\,N{m^{ - 2}}.$$ Each side of the cube is shortened by $$1\% .$$ Find $$x$$ if $$1.67 \times {10^x}\,N/{m^2}$$ be the bulk modulus of elasticity of the cube.
A
7
B
11
C
12
D
15
Answer :
7
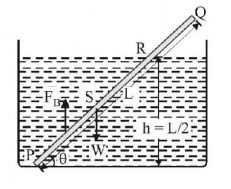
116. A uniform rod of density $$\rho $$ is placed in a wide tank containing a liquid of density $${\rho _0}\left( {{\rho _0} > \rho } \right).$$ The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle $$\theta $$ with the horizontal, then:
A
$$\sin \theta = \frac{1}{2}\sqrt {\frac{{{\rho _0}}}{\rho }} $$
B
$$\sin \theta = \frac{1}{2}.\frac{{{\rho _0}}}{\rho }$$
C
$$\sin \theta = \sqrt {\frac{\rho }{{{\rho _0}}}} $$
D
$$\sin \theta = \frac{{{\rho _0}}}{\rho }$$
Answer :
$$\sin \theta = \frac{1}{2}\sqrt {\frac{{{\rho _0}}}{\rho }} $$
117. A fluid is in streamline flow across a horizontal pipe of variable area of cross section. For this which of the following statements is correct?
A
The velocity is minimum at the narrowest part of the pipe and the pressure is minimum at the widest part of the pipe
B
The velocity is maximum at the narrowest part of the pipe and pressure is maximum at the widest part of the pipe
C
Velocity and pressure both are maximum at the narrowest part of the pipe
D
Velocity and pressure both are maximum at the widest part of the pipe
Answer :
The velocity is maximum at the narrowest part of the pipe and pressure is maximum at the widest part of the pipe
118. A steel wire of cross-sectional area $$3 \times {10^{ - 6}}{m^2}$$ can with stand a maximum strain of $${10^{ - 3}}.$$ Young's modulus of steel is $$2 \times {10^{11}}\,N/{m^2}.$$ The maximum mass the wire can hold is:
A
$$40\,kg$$
B
$$60\,kg$$
C
$$80\,kg$$
D
$$100\,kg$$
Answer :
$$100\,kg$$
119. A circular tube of mean radius $$8\,cm$$ and thickness $$0.04\,cm$$ is melted up and recast into a solid rod of the same length. The ratio of the torsional rigidities of the circular tube and the solid rod is
A
$$\frac{{{{\left( {8.02} \right)}^4} - {{\left( {7.98} \right)}^4}}}{{{{\left( {0.8} \right)}^4}}}$$
B
$$\frac{{{{\left( {8.02} \right)}^2} - {{\left( {7.98} \right)}^2}}}{{{{\left( {0.8} \right)}^2}}}$$
C
$$\frac{{{{\left( {0.8} \right)}^2}}}{{{{\left( {8.02} \right)}^4} - {{\left( {7.98} \right)}^4}}}$$
D
$$\frac{{{{\left( {0.8} \right)}^2}}}{{{{\left( {8.02} \right)}^3} - {{\left( {7.98} \right)}^2}}}$$
Answer :
$$\frac{{{{\left( {8.02} \right)}^4} - {{\left( {7.98} \right)}^4}}}{{{{\left( {0.8} \right)}^4}}}$$
120. In a hydraulic lift, compressed air exerts a force $${F_1}$$ on a small piston having a radius of $$5\,cm.$$ This pressure is transmitted to a second piston of radius $$15\,cm.$$ If the mass of the load to be lifted is $$1350\,kg,$$ find the value of $${F_1}$$ ? The pressure necessary to accomplish this task is
A
$$1.4 \times {10^5}\,Pa$$
B
$$2 \times {10^5}\,Pa$$
C
$$1.9 \times {10^5}\,Pa$$
D
$$1.9\,Pa$$
Answer :
$$1.9 \times {10^5}\,Pa$$