101.
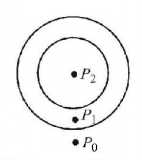
A soap bubble of radius $$R$$ is surrounded by another soap bubble of radius $$2R,$$ as shown. Take surface tension $$= S.$$ Then the pressure inside the smaller soap bubble, in excess of the atmospheric pressure, will be
A
$$\frac{{4S}}{R}$$
B
$$\frac{{3S}}{R}$$
C
$$\frac{{6S}}{R}$$
D
None of these
Answer :
$$\frac{{6S}}{R}$$
102.
What per cent of length of wire increases by applying a stress of $$1\,kg\,{\text{weight}}/m{m^2}$$ on it?
($$Y = 1 \times {10^{11}}\,N/{m^2}$$ and $$1\,kg$$ weight = 9.8 newton)
A
$$0.0067\% $$
B
$$0.0098\% $$
C
$$0.0088\% $$
D
$$0.0078\% $$
Answer :
$$0.0098\% $$
103. Water is flowing continuously from a tap having an internal diameter $$8 \times {10^{ - 3}}m.$$ The water velocity as it leaves the tap is $$0.4\,m{s^{ - 1}}.$$ The diameter of the water stream at a distance $$2 \times {10^{ - 1}}m$$ below the tap is close to:
A
$$7.5 \times {10^{ - 3}}m$$
B
$$9.6 \times {10^{ - 3}}m$$
C
$$3.6 \times {10^{ - 3}}m$$
D
$$5.0 \times {10^{ - 3}}m$$
Answer :
$$3.6 \times {10^{ - 3}}m$$
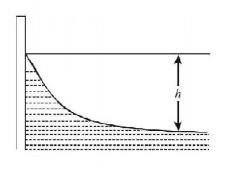
104.
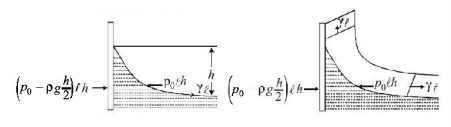
Water of density $$\rho $$ in a clean aquarium forms a meniscus, as illustrated in the figure. Calculate the difference in height $$h$$ between the centre and the edge of the meniscus. The surface tension of water is $$\gamma .$$
A
$$\sqrt {\frac{{2\gamma }}{{\rho g}}} $$
B
$$\sqrt {\frac{\gamma }{{\rho g}}} $$
C
$$\frac{1}{2}\sqrt {\frac{\gamma }{{\rho g}}} $$
D
$$2\sqrt {\frac{\gamma }{{\rho g}}} $$
Answer :
$$\sqrt {\frac{{2\gamma }}{{\rho g}}} $$
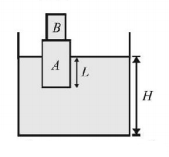
105.
Two wooden blocks $$A$$ and $$B$$ float in a liquid of density $${\rho _L}$$ as shown. The distance $$L$$ and $$H$$ are shown. After some time, block $$B$$ falls into the liquid, so that $$L$$ decreases and $$H$$ increases. If density of block $$B$$ is $${\rho _B},$$ find the correct option.
A
$${\rho _L} = {\rho _B}$$
B
$${\rho _L} > {\rho _B}$$
C
$${\rho _L} < {\rho _B}$$
D
unpredictable
Answer :
$${\rho _L} > {\rho _B}$$
106. The Poisson’s ratio of a material is $$0.5.$$ If a force is applied to a wire of this material, there is a decrease in the cross-sectional area by $$4\% .$$ The percentage increase in the length is :
A
$$1\% $$
B
$$2\% $$
C
$$2.5\% $$
D
$$4\% $$
Answer :
$$4\% $$
107. Drops of liquid of density $$\rho $$ are floating half immersed in a liquid of density $$\sigma .$$ If the surface tension of liquid is $$T,$$ the radius of the drop will be
A
$$\sqrt {\frac{{3T}}{{g\left( {3\rho - \sigma } \right)}}} $$
B
$$\sqrt {\frac{{6T}}{{g\left( {2\rho - \sigma } \right)}}} $$
C
$$\sqrt {\frac{{3T}}{{g\left( {2\rho - \sigma } \right)}}} $$
D
$$\sqrt {\frac{{3T}}{{g\left( {4\rho - 3\sigma } \right)}}} $$
Answer :
$$\sqrt {\frac{{3T}}{{g\left( {2\rho - \sigma } \right)}}} $$
108.
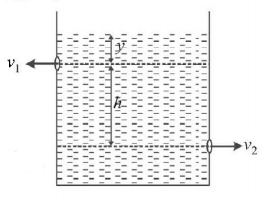
There are two identical small holes $$P$$ and $$Q$$ of area of cross-section $$a$$ on the opposite sides of a tank containing a liquid of density $$\rho .$$ The difference in height between the holes is $$h.$$ Tank is resting on a smooth horizontal surface. Horizontal force which will has to be applied on the tank to keep it in equilibrium is

A
$$gh\rho a$$
B
$$\frac{{2gh}}{{\rho a}}$$
C
$$2\,\rho agh$$
D
$$\frac{{\rho gh}}{a}$$
Answer :
$$2\,\rho agh$$
109. The force exerted by a special compression device is given as function of compression $$x$$ as $${F_x}\left( x \right) = kx\left( {x - \ell } \right)$$ for $$0 \leqslant x \leqslant \ell ,$$ where $$\ell $$ is maximum possible compression and $$k$$ is a constant. The force exerted by the device under compression is maximum when compression is -
A
$$0$$
B
$$\frac{\ell }{4}$$
C
$$\frac{\ell }{{\sqrt 2 }}$$
D
$$\frac{\ell }{2}$$
Answer :
$$\frac{\ell }{2}$$
110.
A water film is formed between two straight parallel wires of $$10\,cm$$ length $$0.5\,cm$$ apart. If the distance between wires is increased by $$1\,mm.$$ What will be the work done ?
(surface tension of water $$= 72\,dyne/cm$$ )
A
$$36\,erg$$
B
$$288\,erg$$
C
$$144\,erg$$
D
$$72\,erg$$
Answer :
$$144\,erg$$