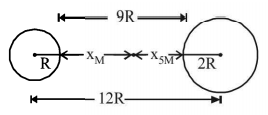
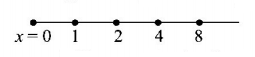151. Two spherical bodies of mass $$M$$ and $$5\,M$$ & radii $$R$$ & $$2\,R$$ respectively are released in free space with initial separation between their centres equal to $$12\,R.$$ If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is-
A
$$2.5\,R$$
B
$$4.5\,R$$
C
$$7.5\,R$$
D
$$1.5\,R$$
Answer :
$$7.5\,R$$
152. The time period of a satellite of earth is 5 hours. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become-
A
10 hours
B
80 hours
C
40 hours
D
20 hours
Answer :
40 hours
153. A geostationary satellite is orbiting the earth at a height of $$5R$$ above that surface of the earth, $$R$$ being the radius of the earth. The time period of another satellite in hour at a height of $$2R$$ from the surface of the earth is
A
$$5$$
B
$$10$$
C
$$6\sqrt 2 $$
D
$$\frac{6}{{\sqrt 2 }}$$
Answer :
$$6\sqrt 2 $$
154. Which graph correctly presents the variation of acceleration due to gravity with the distance from the centre of the earth (radius of the earth $$= {R_E}$$ ) ?
A
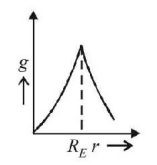

B
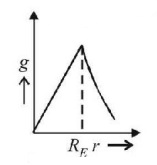

C
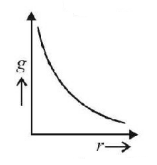

D
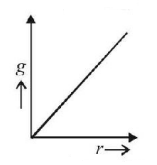

Answer :


155. A satellite of mass $$m$$ revolves around the earth of radius $$R$$ at a height $$x$$ from its surface. If $$g$$ is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
A
$$\frac{{g{R^2}}}{{R + x}}$$
B
$$\frac{{gR}}{{R - x}}$$
C
$$gx$$
D
$${\left( {\frac{{g{R^2}}}{{R + x}}} \right)^{\frac{1}{2}}}$$
Answer :
$${\left( {\frac{{g{R^2}}}{{R + x}}} \right)^{\frac{1}{2}}}$$
156. For a particle inside a uniform spherical shell, the gravitational force on the particle is
A
infinite
B
zero
C
$$\frac{{ - G{m_1}{m_2}}}{{{r^2}}}$$
D
$$\frac{{G{m_1}{m_2}}}{{{r^2}}}$$
Answer :
zero
157. A particle of mass $$M$$ is situated at the centre of a spherical shell of same mass and radius $$a.$$ The gravitational potential at a point situated at $$\frac{a}{2}$$ distance from the centre, will be:
A
$$ - \frac{{3GM}}{a}$$
B
$$ - \frac{{2GM}}{a}$$
C
$$ - \frac{{GM}}{a}$$
D
$$ - \frac{{4GM}}{a}$$
Answer :
$$ - \frac{{3GM}}{a}$$
158. Infinite number of masses, each $$1\,kg$$ are placed along the $$x$$-axis at $$x = \pm 1\,m, \pm 2\,m, \pm 4\,m, \pm 8\,m, \pm 16\,m\,......$$ the magnitude of the resultant gravitational potential in terms of gravitational constant $$G$$ at the orgin $$\left( {x = 0} \right)$$ is
A
$$\frac{G}{2}$$
B
$$G$$
C
$$2G$$
D
$$4G$$
Answer :
$$4G$$
159. If the gravitational force between two objects were proportional to $$\frac{1}{R}$$ (and not as $$\frac{1}{{{R^2}}}$$), where $$R$$ is separation between them, then a particle in circular orbit under such a force would have its orbital speed $$v$$ proportional to
A
$$\frac{1}{{{R^2}}}$$
B
$${R^0}$$
C
$$R$$
D
$$\frac{1}{R}$$
Answer :
$${R^0}$$
160.
Two spheres each of mass $$M$$ are situated at a distance $$2d$$ (see figure). A particle of mass $$m\left( {m < < M} \right)$$ is taken along the path shown in figure. The work done in the process from $$A$$ to $$B$$ is

A
$$\frac{{7GMm}}{d}$$
B
$$\frac{{8GMm}}{d}$$
C
$$ - \frac{{8GMm}}{d}$$
D
zero
Answer :
zero