141. The earth is assumed to be a sphere of radius $$R.$$ A platform is arranged at a height $$R$$ from the surface of the earth. The escape velocity of a body from this platform is $$f{v_e},$$ where $${v_e}$$ is its escape velocity from the surface of the earth. The value of $$f$$ is
A
$$\sqrt 2 $$
B
$$\frac{1}{{\sqrt 2 }}$$
C
$$\frac{1}{3}$$
D
$$\frac{1}{2}$$
Answer :
$$\frac{1}{{\sqrt 2 }}$$
142.
The figure shows elliptical orbit of a planet $$m$$ about the sun $$S.$$ The shaded area $$SCD$$ is twice the shaded area $$SAB.$$ If $${t_1}$$ is the time for the planet to move from $$C$$ to $$D$$ and $${t_2}$$ is the time to move from $$A$$ to $$B$$ then

A
$${t_1} = 4{t_2}$$
B
$${t_1} = 2{t_2}$$
C
$${t_1} = {t_2}$$
D
$${t_1} > {t_2}$$
Answer :
$${t_1} = 2{t_2}$$
143. If $$'g\,'$$ is the acceleration due to gravity on the earth’s surface, the gain in the potential energy of an object of mass $$'m\,'$$ raised from the surface of the earth to a height equal to the radius $$'R\,'$$ of the earth is-
A
$$\frac{1}{4}mgR$$
B
$$\frac{1}{2}mgR$$
C
$$2\,mgR$$
D
$$mgR$$
Answer :
$$\frac{1}{2}mgR$$
144.
The figure shows elliptical orbit of a planet $$m$$ about the sun $$S.$$ The shaded area $$SCD$$ is twice the shaded area $$SAB.$$ If $${t_1}$$ is the time for the planet to move from $$C$$ to $$D$$ and $${t_2}$$ is the time to move from $$A$$ to $$B,$$ then

A
$${t_1} > {t_2}$$
B
$${t_1} = 4{t_2}$$
C
$${t_1} = 2{t_2}$$
D
$${t_1} = {t_2}$$
Answer :
$${t_1} = 2{t_2}$$
145. Consider two solid uniform spherical objects of the same density $$\rho .$$ One has radius $$R$$ and the other has radius $$2R.$$ They are in outer space where the gravitational field from other objects are negligible. If they are arranged with their surface touching, what is the contact force between the objects due to their traditional attraction?
A
$$G{\pi ^2}{R^4}$$
B
$$\frac{{128}}{{81}}G{\pi ^2}{R^4}{\rho ^2}$$
C
$$\frac{{128}}{{81}}G{\pi ^2}$$
D
$$\frac{{128}}{{87}}{\pi ^2}{R^4}G$$
Answer :
$$\frac{{128}}{{81}}G{\pi ^2}{R^4}{\rho ^2}$$
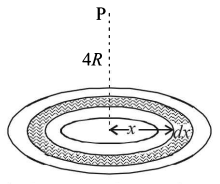
146.
A thin uniform annular disc (see figure) of mass $$M$$ has outer radius $$4R$$ and inner radius $$3R.$$ The work required to take a unit mass from point $$P$$ on its axis to infinity is-

A
$$\frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
B
$$ - \frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
C
$$\frac{{GM}}{{4R}}$$
D
$$\frac{{2GM}}{{5R}}\left( {\sqrt 2 - 1} \right)$$
Answer :
$$\frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
147. Two bodies of masses $$4\,kg$$ and $$9\,kg$$ are separated by a distance of $$60\,cm.$$ A $$1\,kg$$ mass is placed in between these two masses. If the net force on $$1\,kg$$ is zero, then its distance from $$4\,kg$$ mass is
A
$$26\,cm$$
B
$$30\,cm$$
C
$$28\,cm$$
D
$$24\,cm$$
Answer :
$$24\,cm$$
148. Two bodies of masses $$m$$ and $$4 \,m$$ are placed at a distance $$r.$$ The gravitational potential at a point on the line joining them where the gravitational field is zero is:
A
$$ - \frac{{4Gm}}{r}$$
B
$$ - \frac{{6Gm}}{r}$$
C
$$ - \frac{{9Gm}}{r}$$
D
$$Zero$$
Answer :
$$ - \frac{{9Gm}}{r}$$
149. If the distance between the earth and the sun were half its present value, the number of days in a year would have been-
A
$$64.5$$
B
$$129$$
C
$$182.5$$
D
$$730$$
Answer :
$$129$$
150. A body attains a height equal to the radius of the earth. The velocity of the body with which it was projected is
A
$$\sqrt {\frac{{GM}}{R}} $$
B
$$\sqrt {\frac{{2GM}}{R}} $$
C
$$\sqrt {\frac{5}{4}\frac{{GM}}{R}} $$
D
$$\sqrt {\frac{{3GM}}{R}} $$
Answer :
$$\sqrt {\frac{{GM}}{R}} $$