161. In older times, people used to think that the earth was flat. Imagine that the earth is indeed not a sphere of radius $$R,$$ but an infinite plate of thickness $$H.$$ What value of $$H$$ is needed to allow the same gravitational acceleration to be experienced as on the surface of the actual earth? (Assume that the earth’s density is uniform and equal in the two models)
A
$$\frac{{2R}}{3}$$
B
$$\frac{{4R}}{3}$$
C
$$\frac{{8R}}{3}$$
D
$$\frac{{R}}{3}$$
Answer :
$$\frac{{2R}}{3}$$
162.
With what minimum speed should $$m$$ be projected from point $$C$$ in presence of two fixed masses $$M$$ each at $$A$$ and $$B$$ as shown in the figure such that mass $$m$$ should escape the gravitational attraction of $$A$$ and $$B$$

A
$$\sqrt {\frac{{2GM}}{R}} $$
B
$$\sqrt {\frac{{2\sqrt 2 GM}}{R}} $$
C
$$2\sqrt {\frac{{GM}}{R}} $$
D
$$2\sqrt 2 \sqrt {\frac{{GM}}{R}} $$
Answer :
$$\sqrt {\frac{{2\sqrt 2 GM}}{R}} $$
163. The distances of two planets from the sun are $${10^{13}}m$$ and $${10^{12}}m$$ respectively. The ratio of time periods of these two planets is
A
$$\frac{1}{{\sqrt {10} }}$$
B
$$100$$
C
$$10\sqrt {10} $$
D
$$\sqrt {10} $$
Answer :
$$10\sqrt {10} $$
164. Which one of the following plots represents the variation of gravitational field on a particle with distance $$r$$ due to a thin spherical shell of radius $$R$$ ? ($$r$$ is measured from the centre of the spherical shell)
A


B


C


D


Answer :


165. Escape velocity from the earth is $$11.2\,km/s.$$ Another planet of same mass has radius $$\frac{1}{4}$$ times that of the earth. What is the escape velocity from another planet?
A
$$11.2\,km/s$$
B
$$44.8\,km/s$$
C
$$22.4\,km/s$$
D
$$5.6\,km/s$$
Answer :
$$22.4\,km/s$$
166. Assume that the acceleration due to gravity on the surface of the moon is $$0.2$$ times the acceleration due to gravity on the surface of the earth. If $${R_e}$$ is the maximum range of a projectile on the earth's surface, what is the maximum range on the surface of the moon for the same velocity of projection
A
$$0.2\,{R_e}$$
B
$$2\,{R_e}$$
C
$$0.5\,{R_e}$$
D
$$5\,{R_e}$$
Answer :
$$5\,{R_e}$$
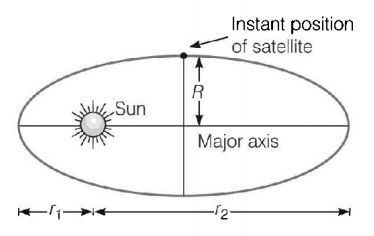
167. The largest and the shortest distance of the earth from the sun are $${r_1}$$ and $${r_2}.$$ Its distance from the sun when it is perpendicular to the major axis of the orbit drawn from the sun
A
$$\frac{{{r_1} + {r_2}}}{4}$$
B
$$\frac{{{r_1} + {r_2}}}{{{r_1} - {r_2}}}$$
C
$$\frac{{2{r_1}{r_2}}}{{{r_1} + {r_2}}}$$
D
$$\frac{{{r_1} + {r_2}}}{3}$$
Answer :
$$\frac{{2{r_1}{r_2}}}{{{r_1} + {r_2}}}$$
168.
A satellite is revolving in a circular orbit at a height $$‘h'$$ from the earth's surface (radius of earth $$R;h < < R$$ ). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth's gravitational field, is close to
: (Neglect the effect of atmosphere.)
A
$$\sqrt {\frac{{gR}}{2}} $$
B
$$\sqrt {gR} \left( {\sqrt 2 - 1} \right)$$
C
$$\sqrt {2gR} $$
D
$$\sqrt {gR} $$
Answer :
$$\sqrt {gR} \left( {\sqrt 2 - 1} \right)$$
169. In a certain region of space, gravitational field is given by $$I = - \left( {\frac{K}{r}} \right).$$ Taking the reference point to be at $$r = {r_0}$$ with $$V = {V_0},$$ find the potential.
A
$$K\log \frac{r}{{{r_0}}} + {V_0}$$
B
$$K\log \frac{{{r_0}}}{r} + {V_0}$$
C
$$K\log \frac{r}{{{r_0}}} - {V_0}$$
D
$$\log \frac{{{r_0}}}{r} - {V_0}r$$
Answer :
$$K\log \frac{r}{{{r_0}}} + {V_0}$$
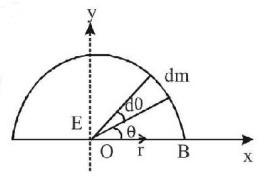
170.
Gravitational field at the centre of a semicircle formed by a thin wire $$AB$$ of mass $$m$$ and length $$\ell $$ is
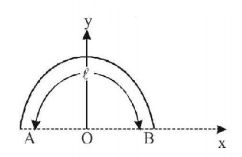
A
$$\frac{{Gm}}{{{\ell ^2}}}$$ along $$+x$$ -axis
B
$$\frac{{Gm}}{{\pi {\ell ^2}}}$$ along $$+y$$ -axis
C
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+x$$ -axis
D
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+y$$ -axis
Answer :
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+y$$ -axis