101. A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass $$ = 5.98 \times {10^{24}}kg$$ ) have to be compressed to be a black hole?
A
$${10^{ - 9}}\,m$$
B
$${10^{ - 6}}\,m$$
C
$${10^{ - 2}}\,m$$
D
$$100\,m$$
Answer :
$${10^{ - 2}}\,m$$
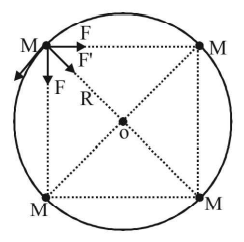
102. Four particles, each of mass $$M$$ and equidistant from each other, move along a circle of radius $$R$$ under the action of their mutual gravitational attraction. The speed of each particle is:
A
$$\sqrt {\frac{{GM}}{R}} $$
B
$$\sqrt {2\sqrt 2 \frac{{GM}}{R}} $$
C
$$\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
D
$$\frac{1}{2}\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
Answer :
$$\frac{1}{2}\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
103. The escape velocity from the surface of the earth is $${v_e}.$$ The escape velocity from the surface of a planet whose mass and radius are three times those of the earth, will be
A
$${v_e}$$
B
$$3{v_e}$$
C
$$9{v_e}$$
D
$$\frac{1}{{3{v_e}}}$$
Answer :
$${v_e}$$
104. An asteriod of mass $$m$$ is approaching earth initially at a distance of $$10{R_e}$$ with speed $${v_i}.$$ It hits the earth with a speed $${v_f}$$ ($${R_e}$$ and $${M_e}$$ are radius and mass of earth), then
A
$$v_f^2 = v_i^2 + \frac{{2Gm}}{{{M_e}R}}\left( {1 - \frac{1}{{10}}} \right)$$
B
$$v_f^2 = v_i^2 + \frac{{2G{M_e}}}{{{R_e}}}\left( {1 + \frac{1}{{10}}} \right)$$
C
$$v_f^2 = v_i^2 + \frac{{2G{M_e}}}{{{R_e}}}\left( {1 - \frac{1}{{10}}} \right)$$
D
$$v_f^2 = v_i^2 + \frac{{2Gm}}{{{R_e}}}\left( {1 - \frac{1}{{10}}} \right)$$
Answer :
$$v_f^2 = v_i^2 + \frac{{2G{M_e}}}{{{R_e}}}\left( {1 - \frac{1}{{10}}} \right)$$
105. If the radius of the earth were to shrink by $$1\% ,$$ with its mass remaining the same, the acceleration due to gravity on the earth’s surface would
A
decrease by $$1\% $$
B
decrease by $$2\% $$
C
increase by $$1\% $$
D
increase by $$2\% $$
Answer :
increase by $$2\% $$
106. The escape velocity for a body projected vertically upwards from the surface of earth is $$11\,km/\,s.$$ If the body is projected at an angle of $${45^ \circ }$$ with the vertical, the escape velocity will be-
A
$$11\sqrt 2 \,km/s$$
B
$$22\,km/s$$
C
$$11\,km/s$$
D
$$\frac{{11}}{{\sqrt 2 }}\,km/s$$
Answer :
$$11\,km/s$$
107. A planet is moving in an elliptical orbit around the sun. If $$T, U, E$$ and $$L$$ stand for its kinetic energy, gravitational potential energy, total energy and magnitude of angular momentum about the centre of force, which of the following is correct?
A
$$T$$ is conserved
B
$$U$$ is always positive
C
$$E$$ is always negative
D
$$L$$ is conserved but direction of vector $$L$$ changes continuously
Answer :
$$E$$ is always negative
108. The ratio of radii of earth to another planet is $$\frac{2}{3}$$ and the ratio of their mean densities is $$\frac{4}{5}.$$ If an astronaut can jump to a maximum height of $$1.5\,m$$ on the earth, with the same effort, the maximum height he can jump on the planet is
A
$$1\,m$$
B
$$0.8\,m$$
C
$$0.5\,m$$
D
$$1.25\,m$$
Answer :
$$0.8\,m$$
109. Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will
A
keep floating at the same distance between them
B
move towards each other
C
move away from each other
D
will become stationary
Answer :
move towards each other
110. A satellite is launched in the equatorial plane in such a way that it can transmit signals upto $${60^ \circ }$$ latitude on the earth. The angular velocity of the satellite is
A
$$\sqrt {\frac{{GM}}{{8{R^3}}}} $$
B
$$\sqrt {\frac{{GM}}{{2{R^3}}}} $$
C
$$\sqrt {\frac{{GM}}{{4{R^3}}}} $$
D
$$\sqrt {\frac{{3\sqrt 3 GM}}{{8{R^3}}}} $$
Answer :
$$\sqrt {\frac{{GM}}{{8{R^3}}}} $$