111. The kinetic energy needed to project a body of mass $$m$$ from the earth surface (radius $$R$$ ) to infinity is-
A
$$\frac{{mgR}}{2}$$
B
$$2 \,mgR$$
C
$$mgR$$
D
$$\frac{{mgR}}{4}$$
Answer :
$$mgR$$
112. Average density of the earth-
A
Is a complex function of $$g$$
B
does not depend on $$g$$
C
is inversely proportional to $$g$$
D
is directly proportional to $$g$$
Answer :
is directly proportional to $$g$$
113.
The figure shows a planet in elliptical orbit around the sun $$S.$$ Where is the kinetic energy of the planet maximum?
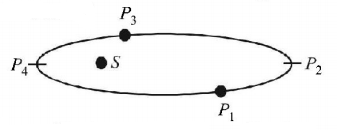
A
$${P_1}$$
B
$${P_2}$$
C
$${P_3}$$
D
$${P_4}$$
Answer :
$${P_4}$$
114. The escape velocity from the earth is $$11.2\,km/s.$$ If a body is to be projected in a direction making an angle $${45^ \circ }$$ to the vertical, then the escape velocity is
A
$$11.2 \times 2\,km/s$$
B
$$11.2\,km/s$$
C
$$\frac{{11.2}}{{\sqrt 2 }}km/s$$
D
$$11.2\sqrt 2 \,km/s$$
Answer :
$$11.2\,km/s$$
115. A roller coaster is designed such that riders experience “weightlessness” as they go round the top of a hill whose radius of curvature is $$20\,m.$$ The speed of the car at the top of the hill is between
A
$$14\,m/s$$ and $$15\,m/s$$
B
$$15\,m/s$$ and $$16\,m/s$$
C
$$16\,m/s$$ and $$17\,m/s$$
D
$$13\,m/s$$ and $$14\,m/s$$
Answer :
$$14\,m/s$$ and $$15\,m/s$$
116.
From a sphere of mass $$M$$ and radius $$R,$$ a smaller sphere of radius $$\frac{R}{2}$$ is carved out such that the cavity made in the original sphere is between its centre and the periphery (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is $$3R,$$ the gravitational force between the two sphere is
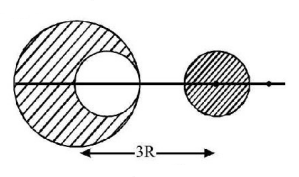
A
$$\frac{{41\,G{M^2}}}{{3600\,{R^2}}}$$
B
$$\frac{{41\,G{M^2}}}{{450\,{R^2}}}$$
C
$$\frac{{59\,G{M^2}}}{{450\,{R^2}}}$$
D
$$\frac{{G{M^2}}}{{225\,{R^2}}}$$
Answer :
$$\frac{{41\,G{M^2}}}{{3600\,{R^2}}}$$
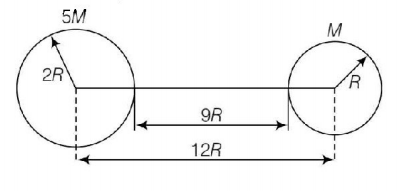
117. Two spherical bodies of masses $$M$$ and $$5M$$ and radii $$R$$ and $$2R$$ are released in free space with initial separation between their centres equal to $$12\,R.$$ If they attract each other due to gravitational force only, then the distance covered by the smaller body before collision is
A
$$2.5\,R$$
B
$$4.5\,R$$
C
$$7.5\,R$$
D
$$1.5\,R$$
Answer :
$$7.5\,R$$
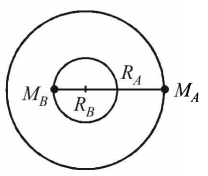
118. A binary star system consists of two stars $$A$$ and $$B$$ which have time period $${T_A}$$ and $${T_B},$$ radius $${R_A}$$ and $${R_B}$$ and mass $${M_A}$$ and $${M_B}.$$ Then-
A
$${\text{if}}\,\,{\mkern 1mu} {T_A} > {T_B}\,{\mkern 1mu} {\text{then }}{\mkern 1mu} {R_A} > {R_B}$$
B
$${\text{if}}\,\,{\mkern 1mu} {T_A} > {T_B}\,{\mkern 1mu} {\text{then }}{\mkern 1mu} {M_A} > {M_B}$$
C
$${\left( {\frac{{{T_A}}}{{{T_B}}}} \right)^2} = {\left( {\frac{{{R_A}}}{{{R_B}}}} \right)^3}$$
D
$${T_A} = {T_B}$$
Answer :
$${T_A} = {T_B}$$
119. The radii of circular orbits of two satellites $$A$$ and $$B$$ of the earth are $$4R$$ and $$R,$$ respectively. If the speed of satellite $$A$$ is $$3v,$$ then the speed of satellite $$B$$ will be
A
$$\frac{{3v}}{4}$$
B
$$6v$$
C
$$12v$$
D
$$\frac{{3v}}{2}$$
Answer :
$$6v$$
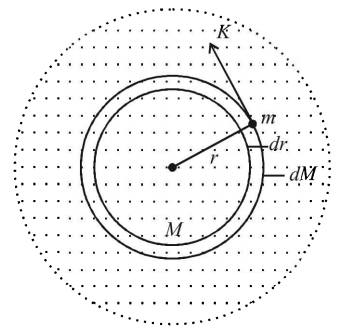
120.
Consider a spherical gaseous cloud of mass density $$\rho \left( r \right)$$ in a free space where $$r$$ is the radical distance from its center. The gaseous cloud is made of particles of equal mass $$m$$ moving in circular orbits about the common centre with the same kinetic energy $$K.$$ The force acting on the particles is their mutual gravitational force. If $$\rho \left( r \right)$$ is constant in time. The particle number density $$n\left( r \right) = \rho \left( r \right)/m$$ is-
[$$G$$ is universal gravitational constant]
A
$$\frac{{3K}}{{\pi {r^2}{m^2}G}}$$
B
$$\frac{K}{{2\pi {r^2}{m^2}G}}$$
C
$$\frac{K}{{\pi {r^2}{m^2}G}}$$
D
$$\frac{{3K}}{{6\pi {r^2}{m^2}G}}$$
Answer :
$$\frac{K}{{2\pi {r^2}{m^2}G}}$$