31. Which of the following is not a method for coagulation of lyophobic sols ?
A
Electrophoresis
B
Mixing oppositely charged sols
C
Adding electrolyte
D
Adding a protective colloid
Answer :
Adding a protective colloid
32. In Freundlich adsorption isotherm, the value of $$\frac{1}{n}$$ is
A
between 0 and 1 in all cases
B
between 2 and 4 in all cases
C
1 in case of physical adsorption
D
1 in case of chemisorption
Answer :
between 0 and 1 in all cases
33. Choose the correct statement
A
$$Latex$$ is an example of solid-in-liquid sol
B
$$Latex$$ is a negative sol
C
$$Latex$$ is a positive sol
D
None of the above is correct
Answer :
$$Latex$$ is a negative sol
34. Which is not correct regarding the adsorption of a gas on surface of solid?
A
On increasing temperature adsorption increases continuously
B
Enthalpy and entropy change is negative
C
Adsorption is more for some specific substance
D
Reversible
Answer :
On increasing temperature adsorption increases continuously
35. In an experiment, addition of $$4.0\,ml$$ of $$0.005\,M$$ $$BaC{l_2}$$ to $$16.0\,ml$$ of arsenius sulphide sol just causes the complete coagulation in 2 hrs. The flocculating value of the effective ion is
A
$$C{l^ - },1.0$$
B
$$C{l^ - },2.0$$
C
$$B{a^{2 + }},1.0$$
D
$$B{a^{2 + }},0.5$$
Answer :
$$B{a^{2 + }},1.0$$
36. The values of colligative properties of colloidal solution are of small order in comparison to those shown by true solutions of same concentration because of colloidal particles
A
exhibit enormous surface area
B
remain suspended in the dispersion medium
C
form lyophilic colloids
D
are comparatively less in number
Answer :
are comparatively less in number
37. A chemical reaction is catalyzed by a catalyst $$X.$$ Hence $$X$$
A
reduces enthalpy of the reaction
B
decreases rate constant of the reaction
C
increases activation energy of the reaction
D
does not affect equilibrium constant of the reaction
Answer :
does not affect equilibrium constant of the reaction
38. Select incorrect statement :
A
Micelles are associated colloids
B
The electrical charge on a colloid particle is indicated by electrophoresis
C
Formation of micelles takes place above Kraft temperature
D
Formation of micelles takes place below $$CMC$$
Answer :
Formation of micelles takes place below $$CMC$$
39. Under the influence of an electric field, the particles in a sol migrate towards cathode. The coagulation of the same sol is studied using $$NaCl,N{a_2}S{O_4}$$ and $$N{a_3}P{O_4}$$ solutions. Their coagulating values will be in maximum for :
A
$$NaCl$$
B
$$N{a_2}S{O_4}$$
C
$$N{a_3}P{O_4}$$
D
$${\text{same for all}}$$
Answer :
$$NaCl$$
40.
Adsorption of a gas follows Freundlich adsorption isotherm. In the given plot, $$x$$ is the mass of the gas adsorbed on mass m of the adsorbent at pressure $$p.$$ $$\frac{x}{m}$$ is proportional to :
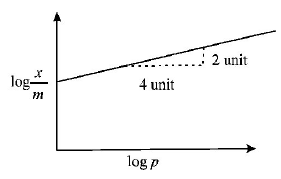
A
$${p^2}$$
B
$${p^{\frac{1}{4}}}$$
C
$${p^{\frac{1}{2}}}$$
D
$$p$$
Answer :
$${p^{\frac{1}{2}}}$$