291. A current of $$2.0\,A$$ passed for 5 hours through a molten metal salt deposits $$22.2\,g$$ of metal $$\left( {At\,wt. = 177} \right).$$ The oxidation state of the metal in the metal salt is
A
+1
B
+2
C
+3
D
+4
Answer :
+3
292. The reduction potential of hydrogen half-cell will be negative if :
A
$$p\left( {{H_2}} \right) = 1\,{\text{atm}}\,{\text{and}}\left[ {{H^ + }} \right] = 2.0\,M$$
B
$$p\left( {{H_2}} \right) = 1\,{\text{atm}}\,{\text{and}}\left[ {{H^ + }} \right] = 1.0\,M$$
C
$$p\left( {{H_2}} \right) = 2\,{\text{atm}}\,{\text{and}}\left[ {{H^ + }} \right] = 1.0\,M$$
D
$$p\left( {{H_2}} \right) = 2\,{\text{atm}}\,{\text{and}}\left[ {{H^ + }} \right] = 2.0\,M$$
Answer :
$$p\left( {{H_2}} \right) = 2\,{\text{atm}}\,{\text{and}}\left[ {{H^ + }} \right] = 1.0\,M$$
293. A dilute aqueous solution of $$N{a_2}S{O_4}$$ is electrolyzed using platinum electrodes. The products at the anode and cathode are :
A
$${O_2},{H_2}$$
B
$${S_2}O_8^{2 - },Na$$
C
$${O_2},Na$$
D
$${S_2}O_8^{2 - },{H_2}$$
Answer :
$${O_2},{H_2}$$
294. Mark the correct relationship from the following :
A
Equilibrium constant is related to $$emf$$ as $$\log \,K = \frac{{nFE}}{{2.303\,RT}}$$
B
$$EMF$$ of a cell $$Zn\left| {Zn_{\left( {{a_1}} \right)}^{2 + }} \right|\left| {Cu_{\left( {{a_2}} \right)}^{2 + }} \right|Cu$$ is $$E = {E^ \circ } - \frac{{0.591}}{n}\log \frac{{\left[ {{a_2}} \right]}}{{\left[ {{a_1}} \right]}}$$
C
Nernst equation is $${E_{{\text{cell}}}} = $$ $$E_{{\text{cell}}}^ \circ - \frac{{0.0591}}{n}\log \frac{{\left[ {{\text{Products}}} \right]}}{{\left[ {{\text{Reactants}}} \right]}}$$
D
For the electrode $$\frac{{{M^{n + }}}}{M}$$ at $$298\,K;$$ $$E = {E^ \circ } + \frac{{0.591}}{n}\log \left[ {{M^{n + }}} \right]$$
Answer :
Nernst equation is $${E_{{\text{cell}}}} = $$ $$E_{{\text{cell}}}^ \circ - \frac{{0.0591}}{n}\log \frac{{\left[ {{\text{Products}}} \right]}}{{\left[ {{\text{Reactants}}} \right]}}$$
295.
$$AgN{O_3}\left( {aq.} \right)$$ was added to an aqueous $$KCl$$ solution gradually and the conductivity of the solution was measured. The plot of conductance $$\left( \Lambda \right)$$ versus the volume of $$AgN{O_3}\left( {aq.} \right)$$
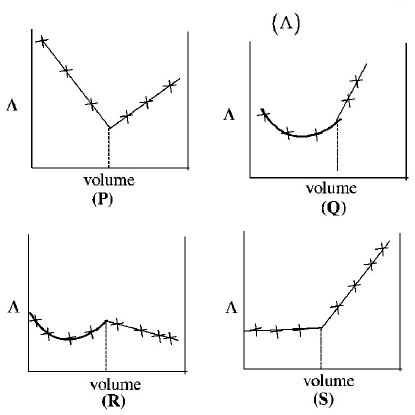
A
$$(P)$$
B
$$(Q)$$
C
$$(R)$$
D
$$(S)$$
Answer :
$$(S)$$
296. The electrode potential $${E_{\left( {\frac{{Z{n^{2 + }}}}{{Zn}}} \right)}}$$ of a zinc electrode at $${25^ \circ }C$$ with an aqueous solution of $$0.1\,M\,ZnS{O_4}$$ is $$\left[ {E_{\left( {{{Z{n^{2 + }}} \over {Zn}}} \right)}^ \circ = - 0.76\,V.{\rm{Assume}}\,{{2.303RT} \over F} = 0.06\,{\rm{at}}\,298\,K} \right].$$
A
$$+0.73$$
B
$$-0.79$$
C
$$-0.82$$
D
$$-0.70$$
Answer :
$$-0.79$$
297. $$4.5$$ $$g$$ of aluminium ( atomic mass $$27u$$ ) is deposited at cathode from $$A{l^{3 + }}$$ solution by a certain quantity of electric charge. The volume of hydrogen produced at $$STP$$ from $${H^ + }\,ions$$ in solution by the same quantity of electric charge will be
A
44.8$$\,L$$
B
22.4$$\,L$$
C
11.2$$\,L$$
D
5.6$$\,L$$
Answer :
5.6$$\,L$$
298. Which of the following is not an application of electrochemical series?
A
To compare the relative oxidising and reducing power of substances.
B
To predict evolution of hydrogen gas on reaction of metal with acid.
C
To predict spontaneity of a redox reaction.
D
To calculate the amount of metal deposited on cathode.
Answer :
To calculate the amount of metal deposited on cathode.
299.
On the basis of the following $${E^ \circ }$$ values, the strongest oxidising agent is
$${\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{4 - }} \to {\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{3 - }} + {e^ - };$$ $${E^ \circ } = - 0.35\,V$$
$$F{e^{2 + }} \to F{e^{3 + }} + {e^ - };$$ $${E^ \circ } = - 0.77\,V$$
A
$${\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{4 - }}$$
B
$$F{e^{2 + }}$$
C
$$F{e^{3 + }}$$
D
$${\left[ {Fe{{\left( {CN} \right)}_6}} \right]^{3 - }}$$
Answer :
$$F{e^{3 + }}$$
300. On passing current through two cells, connected in series containing solution of $$AgN{O_3}$$ and $$CuS{O_4},0.18\,g$$ of $$Ag$$ is deposited. The amount of the $$Cu$$ deposited is :
A
0.529$$\,g$$
B
10.623$$\,g$$
C
0.0529$$\,g$$
D
1.2708$$\,g$$
Answer :
0.0529$$\,g$$