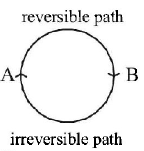
61. The internal energy change when a system goes from state $$A$$ to $$B$$ is $$40 kJ/mole.$$ If the system goes from $$A$$ to $$B$$ by a reversible path and returns to state $$A$$ by an irreversible path what would be the net change in internal energy ?
A
$$> 40 kJ$$
B
$$< 40 kJ$$
C
$$Zero$$
D
$$40 kJ$$
Answer :
$$Zero$$
62. When the system does not exchange heat with the surroundings, the process is
A
isothermal
B
adiabatic
C
thermal
D
isochoric
Answer :
adiabatic
63. The standard enthalpy of formation of $$N{H_3}$$ is $$ - 46.0\,kJ/mol.$$ If the enthalpy of formation of $${H_2}$$ from its atoms is $$ - 436\,kJ/mol$$ and that of $${N_2}$$ is $$ - 712\,kJ/mol,$$ the average bond enthalpy of $$N - H$$ bond in $$N{H_3}$$ is :
A
$$ - 1102\,kJ/mol$$
B
$$ - 964\,kJ/mol$$
C
$$ + 352\,kJ/mol$$
D
$$ + 1056\,kJ/mol$$
Answer :
$$ - 964\,kJ/mol$$
64. What is the amount of heat ( in Joules ) absorbed by $$18\,g$$ of water initially at room temperature heated to $${100^ \circ }C?$$ If $$10\,g$$ of $$Cu$$ is added to this water , than decrease in temperature ( in Kelvin ) of water was found to be? $$C\left( {p,m} \right)$$ for water $$75.32\,J/mol\,K;C\left( {p,m} \right)$$ for $$Cu = 24.47\,J/mol\,K.$$
A
5649, 369
B
5544, 324
C
5278, 342
D
3425, 425
Answer :
5649, 369
65. Which of the following statements/relationships is not correct in thermodynamic changes?
A
$$\Delta U = 0$$ ( isothermal reversible expansion of a gas )
B
$$w = - nRT\,\,{\text{ln}}\,\,\frac{{{V_2}}}{{{V_1}}}$$ ( isothermal reversible expansion of an ideal gas )
C
$$w = nRT\,\,{\text{ln}}\,\,\frac{{{V_2}}}{{{V_1}}}$$ ( isothermal reversible
expansion of an ideal gas )
D
For a system of constant volume heat involved directly changes to internal energy.
Answer :
$$w = nRT\,\,{\text{ln}}\,\,\frac{{{V_2}}}{{{V_1}}}$$ ( isothermal reversible
expansion of an ideal gas )
66. Which of the following is not correct ?
A
$$\Delta G$$ is zero for a reversible reaction.
B
$$\Delta G$$ is positive for a spontaneous reaction.
C
$$\Delta G$$ is negative for a spontaneous reaction.
D
$$\Delta G$$ is positive for a non-spontaneous reaction.
Answer :
$$\Delta G$$ is positive for a spontaneous reaction.
67. For a sample of perfect gas when its pressure is changed isothermally from $${p_i}$$ to $${p_f},$$ the entropy change is given by
A
$$\Delta S = nR\,\ln \left( {\frac{{{p_f}}}{{{p_i}}}} \right)$$
B
$$\Delta S = nR\,\ln \left( {\frac{{{p_i}}}{{{p_f}}}} \right)$$
C
$$\Delta S = nRT\,\ln \left( {\frac{{{p_f}}}{{{p_i}}}} \right)$$
D
$$\Delta S = RT\,\ln \left( {\frac{{{p_i}}}{{{p_f}}}} \right)$$
Answer :
$$\Delta S = nR\,\ln \left( {\frac{{{p_i}}}{{{p_f}}}} \right)$$
68.
For reversible reaction :$${X_{\left( g \right)}} + 3{Y_{\left( g \right)}} \rightleftharpoons 2{Z_{\left( g \right)}};$$ $$\Delta H = - 40\,kJ\,mo{l^{ - 1}}$$
Standard entropies of $$X, Y$$ and $$Z$$ are $$60, 40$$ and $$50\,J\,{K^{ - 1}}\,mo{l^{ - 1}}$$ respectively. The temperature at which the above reaction is in equilibrium is
A
273$$\,K$$
B
600$$\,K$$
C
500$$\,K$$
D
400$$\,K$$
Answer :
500$$\,K$$
69. For the reaction taking place at certain temperature $$N{H_2}COON{H_4}\left( s \right) \rightleftharpoons $$ $$2N{H_3}\left( g \right) + C{O_2}\left( g \right),$$ if equilibrium pressure is $$3X$$ $$bar$$ then $${\Delta _r}{G^ \circ }$$ would be
A
$$ - RT\,\,{\text{ln}}\,\,9 - 3RT\,\,{\text{ln}}\,\,X$$
B
$$RT\,\,{\text{ln}}\,\,4 - 3RT\,\,{\text{ln}}\,\,X$$
C
$$ - 3RT\,\,{\text{ln}}\,\,X$$
D
$${\text{None of these}}$$
Answer :
$${\text{None of these}}$$
70. In thermodynamics, which one of the following properties is not an intensive property ?
A
Pressure
B
Temperature
C
Volume
D
Density
Answer :
Volume