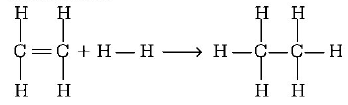161. Change in enthalpy for reaction, $$2{H_2}{O_2}\left( l \right) \to 2{H_2}O\left( l \right) + {O_2}\left( g \right)$$ if heat of formation of $${H_2}{O_2}\left( l \right)$$ and $${H_2}O\left( l \right)$$ are $$-188$$ and $$ - 286\,kJ/mol$$ respectively is
A
$$ - \,196\,kJ/mol$$
B
$$ + \,196\,kJ/mol$$
C
$$ + \,948\,kJ/mol$$
D
$$ - \,948\,kJ/mol$$
Answer :
$$ - \,196\,kJ/mol$$
162. $$36\,mL$$ of pure water takes 100 sec to evaporate from a vessel and heater connected to an electric source which delivers $$806\,watt.$$ The $$\Delta {H_{vap}}$$ of $${H_2}O$$ is :
A
$$40.3\,kJ/mol$$
B
$$43.2\,kJ/mol$$
C
$$4.03\,kJ/mol$$
D
$${\text{None of these}}$$
Answer :
$$40.3\,kJ/mol$$
163. How much heat is evolved if 3.2$$\,g$$ of methane is burnt and if the heat of combustion of methane is $$ - 880\,kJ\,mo{l^{ - 1}}?$$
A
88$$\,kJ$$
B
264$$\,kJ$$
C
176$$\,kJ$$
D
440$$\,kJ$$
Answer :
176$$\,kJ$$
164. For a given reaction, $$\Delta H = 35.5\,kJ\,mo{l^{ - 1}}$$ and $$\Delta S = 83.6\,J{K^{ - 1}}mo{l^{ - 1}}.$$ The reaction is spontaneous at : ( Assume that $$\Delta H$$ ans $$\Delta S$$ do not vary with temperature )
A
$$T < 425\,K$$
B
$$T > 425\,K$$
C
$${\text{all ternperatures}}$$
D
$$T > 298K$$
Answer :
$$T > 425\,K$$
165.
Which of the following are not state functions?
$$\eqalign{
& \left( {\text{i}} \right)\,q + W \cr
& \left( {{\text{ii}}} \right)\,q \cr
& \left( {{\text{iii}}} \right)\,W \cr
& \left( {{\text{iv}}} \right)\,H - TS \cr} $$
A
(i) and (iv)
B
(ii), (iii) and (iv)
C
(i), (ii) and (iii)
D
(ii) and (iii)
Answer :
(ii) and (iii)
166.
For the auto-ionization of water at $${25^ \circ }C,$$ $${H_2}O\left( l \right) \rightleftharpoons {H^ + }\left( {aq} \right) + O{H^ - }\left( {aq} \right)$$ equilibrium constant is $${10^{ - 14}}.$$
What is $$\Delta {G^ \circ }$$ for the process?
A
$$ \simeq 8 \times {10^4}\,J\,mo{l^{ - 1}}$$
B
$$ \simeq 3.5 \times {10^4}\,J\,mo{l^{ - 1}}$$
C
$$ \simeq 2 \times {10^4}\,J\,mo{l^{ - 1}}$$
D
$${\text{None of these}}$$
Answer :
$$ \simeq 8 \times {10^4}\,J\,mo{l^{ - 1}}$$
167.
Given :
$$\eqalign{
& {\text{(i)}}\,{H_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to {H_2}O\left( l \right); \cr
& \Delta {H^ \circ }_{298K} = - 285.9\,kJ\,mo{l^{ - 1}} \cr
& {\text{(ii)}}\,{H_2}\left( g \right) + \frac{1}{2}{O_2}\left( g \right) \to {H_2}O\left( g \right); \cr
& \Delta {H^ \circ }_{298K} = - 241.8\,kJ\,mo{l^{ - 1}} \cr} $$
The molar enthalpy of vapourisation of water will be :
A
$$241.8\,kJ\,mo{l^{ - 1}}$$
B
$$22.0\,kJ\,mo{l^{ - 1}}$$
C
$$44.1\,kJ\,mo{l^{ - 1}}$$
D
$$527.7\,kJ\,mo{l^{ - 1}}$$
Answer :
$$44.1\,kJ\,mo{l^{ - 1}}$$
168. Hydrogen has an ionisation energy of $$1311\,kJ\,mo{l^{ - 1}}$$ and for chlorine it is $$1256\,kJ\,mo{l^{ - 1}}.$$ Hydrogen forms $${H^ + }\left( {aq} \right)ions$$ but chlorine does not form $$C{l^ + }\left( {aq} \right)ions$$ because
A
$${H^ + }$$ has lower hydration enthalpy
B
$$C{l^ + }$$ has lower hydration enthalpy
C
$$Cl$$ has high electron affinity
D
$$Cl$$ has high electronegativity
Answer :
$$C{l^ + }$$ has lower hydration enthalpy
169.
From the following bond energies
$$\eqalign{
& H - H\,{\text{bond energy}}:431.37\,kJ\,mo{l^{ - 1}} \cr
& C = C\,{\text{bond energy}}:606.10\,kJ\,mo{l^{ - 1}} \cr
& C - C\,{\text{bond energy}}:336.49\,kJ\,mo{l^{ - 1}} \cr
& C - H\,{\text{bond energy}}:410.50\,kJ\,mo{l^{ - 1}}\, \cr} $$
Enthalpy for the reaction,

will be
A
$$1523.6\,kJ\,mo{l^{ - 1}}$$
B
$$ - 243.6\,kJ\,mo{l^{ - 1}}$$
C
$$ - 120.0\,kJ\,mo{l^{ - 1}}$$
D
$$553.0\,kJ\,mo{l^{ - 1}}$$
Answer :
$$ - 120.0\,kJ\,mo{l^{ - 1}}$$
170. At dynamic equilibrium the reaction on both sides occur at the same rate and the mass on both sides of the equilibrium does not undergo any change. This condition can be achieved only when the value of $$\Delta G$$ is
A
$$-1$$
B
$$+1$$
C
$$+2$$
D
$$0$$
Answer :
$$0$$