81. Units of rate constant of first and zero order reactions in terms of molarity $$M$$ unit are respectively
A
$${\sec ^{ - 1}},M.{\sec ^{ - 1}}$$
B
$${\sec ^{ - 1}},M$$
C
$$M.{\sec ^{ - 1}},{\sec ^{ - 1}}$$
D
$$M,{\sec ^{ - 1}}$$
Answer :
$${\sec ^{ - 1}},M.{\sec ^{ - 1}}$$
82. The rate of first order reaction is \[1.5\times {{10}^{-2}}mol\,{{L}^{-1}}{{\min }^{-1}}\] at $$0.5\,M$$ concentration of the reactant. The half-life of the reaction is
A
$$0.383\,\min $$
B
$$23.1\,\min $$
C
$$8.73\,\min $$
D
$$7.53\,\min $$
Answer :
$$23.1\,\min $$
83.
Nitrogen dioxide $$\left( {N{O_2}} \right)$$ dissociates into nitric oxide $$(NO)$$ and oxygen $$\left( {{O_2}} \right)$$ as follows : $$2N{O_2} \to 2NO + {O_2}$$
If the rate of decrease of concentration of $$N{O_2}$$ is $$6.0 \times {10^{ - 12}}\,mol\,{L^{ - 1}}{s^{ - 1}}.$$ What will be the rate of increase of concentration of $${O_2}?$$
A
$$3 \times {10^{ - 12}}\,mol\,{L^{ - 1}}{s^{ - 1}}$$
B
$$6 \times {10^{ - 12}}\,mol\,{L^{ - 1}}\,{s^{ - 1}}$$
C
$$1 \times {10^{ - 12}}\,mol\,{L^{ - 1}}\,{s^{ - 1}}$$
D
$$1.5 \times {10^{ - 12}}\,mol\,{L^{ - 1}}\,{s^{ - 1}}$$
Answer :
$$3 \times {10^{ - 12}}\,mol\,{L^{ - 1}}{s^{ - 1}}$$
84. The rate of a chemical reaction doubles for every $${10^ \circ }C$$ rise of temperature. If the temperature is raised by $${50^ \circ }C,$$ the rate of the reaction increases by about :
A
10 times
B
24 times
C
32 times
D
64 times
Answer :
32 times
85.
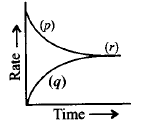
For a reversible reaction, $$A + B \rightleftharpoons C + D,$$ the graph for rate of reaction with time is given below. Mark the terms $$(p), (q)$$ and $$(r).$$
A
$$(p)$$ - rate of backward reaction, $$(q)$$ - rate of forward reaction, $$(r)$$ - equilibrium
B
$$(p)$$ - rate of forward reaction, $$(q)$$ - rate of backward reaction, $$(r)$$ - equilibrium
C
$$(p)$$ - concentration of products, $$(q)$$ - concentration
of reactants, $$(r)$$ - rate of reaction
D
$$(p)$$ - instantaneous rate of reaction, $$(q)$$ - variation of rate, $$(r)$$ - average rate of reaction
Answer :
$$(p)$$ - rate of forward reaction, $$(q)$$ - rate of backward reaction, $$(r)$$ - equilibrium
86.
In a pseudo first order hydrolysis of ester in water, the following results were obtained.
$$t/s$$
0
30
60
90
Ester/$$mol\,{L^{ - 1}}$$
0.55
0.31
0.17
0.085
What will be the average rate of reaction between the time interval 30 to 60 seconds?
A
$$1.91 \times {10^{ - 2}}\,{s^{ - 1}}$$
B
$$4.67 \times {10^{ - 3}}\,mol\,{L^{ - 1}}\,{s^{ - 1}}$$
C
$$1.98 \times {10^{ - 3}}\,{s^{ - 1}}$$
D
$$2.07 \times {10^{ - 2}}\,{s^{ - 1}}$$
Answer :
$$4.67 \times {10^{ - 3}}\,mol\,{L^{ - 1}}\,{s^{ - 1}}$$
87. Decomposition of $${H_2}{O_2}$$ follows a first order reaction. In fifty minutes the concentration of $${H_2}{O_2}$$ decreases from 0.5 to $$0.125 M$$ in one such decomposition. When the concentration of $${H_2}{O_2}$$ reaches $$0.05 M,$$ the rate of formation of $${O_2}$$ will be :
A
$$2.66\,L\,\min {\,^{ - 1}}at\,STP$$
B
$$1.34 \times {10^{ - 2}}\,mol\,\min {\,^{ - 1}}$$
C
$$6.96 \times {10^{ - 2}}\,mol\,\min {\,^{ - 1}}$$
D
$$6.93 \times {10^{ - 4}}\,mol\,\min {\,^{ - 1}}$$
Answer :
$$6.93 \times {10^{ - 4}}\,mol\,\min {\,^{ - 1}}$$
88. For the reaction, $$2A + B \to 3C + D$$ which of the following does not express the reaction rate?
A
$$ - \frac{{d\left[ C \right]}}{{3dt}}$$
B
$$ - \frac{{d\left[ B \right]}}{{dt}}$$
C
$$\frac{{d\left[ D \right]}}{{dt}}$$
D
$$ - \frac{{d\left[ A \right]}}{{2dt}}$$
Answer :
$$ - \frac{{d\left[ C \right]}}{{3dt}}$$
89.
A following mechanism has been proposed for a reaction
$$\eqalign{
& 2A + B \to D + E \cr
& A + B \to C + D\left( {{\text{slow}}} \right) \cr
& A + C \to E\left( {{\text{fast}}} \right) \cr} $$
The rate law expression for the reaction is :
A
$$r = k{\left[ A \right]^2}\left[ B \right]$$
B
$$r = k\left[ A \right]\left[ B \right]$$
C
$$r = k{\left[ A \right]^2}$$
D
$$r = k\left[ A \right]\left[ C \right]$$
Answer :
$$r = k\left[ A \right]\left[ B \right]$$
90. The decomposition of a hydrocarbon follows the equation $$k = \left( {4.5 \times {{10}^{11}}\,{s^{ - 1}}} \right){e^{ - \frac{{28000\,K}}{T}}}.$$ What will be the value of activation energy?
A
$$669\,kJ\,mo{l^{ - 1}}$$
B
$$232.79\,kJ\,mo{l^{ - 1}}$$
C
$$4.5 \times {10^{11}}\,kJ\,mo{l^{ - 1}}$$
D
$$28000\,kJ\,mo{l^{ - 1}}$$
Answer :
$$232.79\,kJ\,mo{l^{ - 1}}$$