71. The value of rate constant of a pseudo first order reaction __________.
A
depends on the concentration of reactants present in small amount
B
depends on the concentration of reactants present in excess
C
is independent of the concentration of reactants
D
depends only on temperature
Answer :
depends on the concentration of reactants present in excess
72. For a first order reaction \[A\to B\] the reaction rate at reactant concentration of \[0.01\,M\] is found to be $$2.0 \times {10^{ - 5}}mol\,{L^{ - 1}}{s^{ - 1}}.$$ The half life period of the reaction is
A
30$$\,s$$
B
220$$\,s$$
C
300$$\,s$$
D
347$$\,s$$
Answer :
347$$\,s$$
73. In respect of the equation $$k = A{e^{ - \,\frac{{{E_a}}}{{RT}}}}$$ in chemical kinetics, which one of the following statements is correct ?
A
$$A$$ is adsorption factor
B
$${E_a}$$ is energy of activation
C
$$R$$ is Rydberg’s constant
D
$$k$$ is equilibrium constant
Answer :
$${E_a}$$ is energy of activation
74. The number of neutrons accompanying the formation of $$_{54}^{139}Xe\,\,$$ and $$_{38}^{94}\,Sr$$ from the absorption of a slow neutron by $$_{92}^{139}U,$$ followed by nuclear fission is,
A
0
B
2
C
1
D
3
Answer :
3
75.
The given plots represents the variation of the concentration of a reactant R with time for two different reactions (i) and (ii) The respective orders of the reactions are :
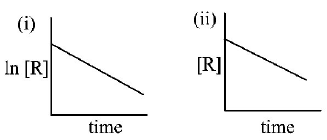
A
1, 0
B
1, 1
C
0, 1
D
0, 2
Answer :
1, 0
76.
Consider the reaction : $$C{l_{2\left( {aq} \right)}} + {H_2}{S_{\left( {aq} \right)}} \to {S_{\left( s \right)}} + 2H_{\left( {aq} \right)}^ + + 2Cl_{\left( {aq} \right)}^ - $$
The rate of reaction for this reaction is $${\text{Rate}} = k\left[ {C{l_2}} \right]\left[ {{H_2}S} \right]$$
Which of these mechanism is/are consistent with this rate equation?
$$\left( {\text{i}} \right)C{l_2} + {H_2}S \to $$ $${H^ + } + C{l^ - } + C{l^ + } + H{S^ - }\left( {{\text{slow}}} \right)$$
$$\,\,\,\,\,\,C{l^ + } + H{S^ - } \to $$ $${H^ + } + C{l^ - } + S\left( {{\text{fast}}} \right)$$
$$\left( {{\text{ii}}} \right){H_2}S \rightleftharpoons {H^ + } + H{S^ - }$$ $$\left( {{\text{fast equilibrium}}} \right)$$
$$\,\,\,\,\,\,\,C{l_2} + H{S^ - } \to $$ $$2C{l^ - } + {H^ + } + S\left( {{\text{slow}}} \right)$$
A
(i) only
B
(ii) only
C
Both (i) and (ii)
D
Neither (i) nor (ii)
Answer :
(i) only
77. The expression to calculate time required for completion of zero order reaction is
A
$$t = \frac{{\left[ {{R_0}} \right]}}{k}$$
B
$$t = \left[ R \right] - \left[ {{R_0}} \right]$$
C
$$t = \frac{k}{{\left[ {{R_0}} \right]}}$$
D
$$t = \frac{{\left[ {{R_0}} \right] - \left[ R \right]}}{{\left[ {{R_0}} \right]}}$$
Answer :
$$t = \frac{{\left[ {{R_0}} \right]}}{k}$$
78.
What is the activation energy for a reaction if its rate doubles when the temperature is raised from $${20^ \circ }C$$ to $${35^ \circ }C?$$
$$\left( {R = 8.314\,J\,mo{l^{ - 1}}{K^{ - 1}}} \right)$$
A
$$342\,kJ\,mo{l^{ - 1}}$$
B
$$269\,kJ\,mo{l^{ - 1}}$$
C
$$34.7\,kJ\,mo{l^{ - 1}}$$
D
$$15.1\,kJ\,mo{l^{ - 1}}$$
Answer :
$$34.7\,kJ\,mo{l^{ - 1}}$$
79.
For the reaction
$${N_2}{O_5}\left( g \right) \to 2N{O_2}\left( g \right) + \frac{1}{2}\,{O_2}\left( g \right)$$ the value of rate of disappearance of $${N_2}{O_5}$$ is given as $$6.25 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}}.$$ The rate of formation of $$N{O_2}$$ and $${O_2}$$ is given respectively as :
A
$$\eqalign{
& 6.25 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}} \cr
& 6.25 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}} \cr} $$
B
$$\eqalign{
& 1.25 \times {10^{ - 2}}\,mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}} \cr
& 3.125 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}} \cr} $$
C
$$\eqalign{
& 6.25 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}} \cr
& 3.125 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}} \cr} $$
D
$$\eqalign{
& 1.25 \times {10^{ - 2}}mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}} \cr
& 6.25 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}} \cr} $$
Answer :
$$\eqalign{
& 1.25 \times {10^{ - 2}}\,mol\,{L^{ - 1}}{s^{ - 1}}\,{\text{and}} \cr
& 3.125 \times {10^{ - 3}}\,mol\,{L^{ - 1}}{s^{ - 1}} \cr} $$
80. When initial concentration of a reactant is doubled in a reaction, its half-life period is not affected. The order of the reaction is
A
zero
B
first
C
second
D
more than zero but less than first
Answer :
first