11. The rate law for a reaction, $$A + B \to C + D$$ is given by the expression $$k\left[ A \right].$$ The rate of reaction will be
A
doubled on doubling the concentration of $$B$$
B
halved on reducing the concentration of $$A$$ to half
C
decreased on increasing the temperature of reaction
D
unaffected by any change in concentration or temperature.
Answer :
halved on reducing the concentration of $$A$$ to half
12. The half life period for catalytic decomposition of $$A{B_3}$$ at $$50\,mm\,Hg$$ is $$4\,hrs$$ and at $$100\,mm\,Hg$$ it is $$2\,hrs.$$ The order of reaction is
A
1
B
3
C
2
D
0
Answer :
2
13. The rate of a first-order reaction is $$0.04\,mol\,{L^{ - 1}}{s^{ - 1}}$$ at $$10$$ $$sec$$ and $$0.03\,mol\,{L^{ - 1}}{s^{ - 1}}$$ at $$20$$ $$sec$$ after initiation of the reaction. The half-life period of the reaction is
A
34.1$$\,s$$
B
44.1$$\,s$$
C
54.1$$\,s$$
D
24.1$$\,s$$
Answer :
24.1$$\,s$$
14. Consider the reaction, $$A \to B.$$ The concentration of both the reactants and the products varies exponentially with time. Which of the following figures correctly describes the change in concentration of reactants and products with time?
A
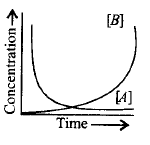

B


C
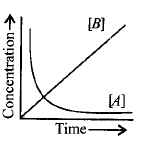

D


Answer :


15. A catalyst lowers the activation energy of a certain reaction from $$83.314$$ to $$75\,kJ\,mo{l^{ - 1}}$$ at $$500\,K.$$ What will be the rate of reaction as compared to uncatalysed reaction? Assume other things being equal.
A
$${\text{Double}}$$
B
$$28\,times$$
C
$$7.38\,times$$
D
$$7.38 \times {10^3}times$$
Answer :
$$7.38\,times$$
16. A first order reaction takes $$40\,\min $$ for $${\text{30% }}$$ decomposition. What will be $${{\text{t}}_{\frac{1}{2}}}?$$
A
77.7 $$\min .$$
B
52.5 $$\min .$$
C
46.2 $$\min .$$
D
22.7 $$\min .$$
Answer :
77.7 $$\min .$$
17. For a first order reaction, $$A \to B,$$ the reaction rate at reactant concentration of $$0.01\,M$$ is found to be $$2.0 \times {10^{ - 5}}mol\,{L^{ - 1}}{s^{ - 1}}.$$ The half-life period of the reaction is
A
220$$\,s$$
B
30$$\,s$$
C
300$$\,s$$
D
347$$\,s$$
Answer :
347$$\,s$$
18. The rate constant of a reaction with a virus is $$3.3 \times {10^{ - 4}}{s^{ - 1}}.$$ Time required for the virus to become $$75\% $$ inactivated is
A
$$35\,\min $$
B
$$70\,\min $$
C
$$105\,\min $$
D
$$17.5\,\min $$
Answer :
$$70\,\min $$
19. If $$'I'$$ is the intensity of absorbed light and $$'C'$$ is the concentration of $$AB$$ for the photochemical process, $$AB +$$ $$hv \to A{B^ * },$$ the rate of formation of $$A{B^ * }$$ is directly proportional to
A
$$C$$
B
$$I$$
C
$${I^2}$$
D
$$C.I$$
Answer :
$$I$$
20. The rate of a gaseous reaction is given by the expression $$k{\left[ A \right]^2}{\left[ B \right]^3}.$$ The volume of the reaction vessel is reduced to one half of the initial volume. What will be the reaction rate as compared to the original rate $$a?$$
A
$$\frac{1}{8}a$$
B
$$\frac{1}{2}a$$
C
$$2a$$
D
$$32a$$
Answer :
$$32a$$