Question
Which of these statements about $${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ is true ?
A.
$${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has no unpaired electrons and will be in a low-spin configuration.
B.
$${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has four unpaired electrons and will be in a low-spin configuration.
C.
$${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has four unpaired electrons and will be in a high-spin configuration.
D.
$${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has no unpaired electrons and will
be in a high-spin configuration.
Answer :
$${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has no unpaired electrons and will be in a low-spin configuration.
Solution :
$$\eqalign{ & {\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }} \cr & C{o^{3 + }} = 1{s^2}\,2{s^2}\,2{p^6}\,3{s^2}\,3{p^6}\,3{d^6} \cr} $$
$$C{N^ - }$$ is a strong field ligand and as it approaches the metal ion, the electrons must pair up.
The splitting of the $$d$$ - orbitals into two sets of orbitals in an octahedral $${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ may be represented as
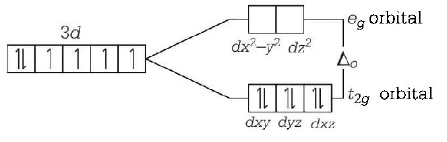
Here, for $${d^6}\,ions,$$ three electrons first enter orbitals with parallel spin put the remaining may pair up in $${t_{2g}}$$ orbital giving rise to low spin complex ( strong ligand ) field.
$$\therefore \,\,{\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has no unpaired electron and will be in a low spin configuration.
$$\eqalign{ & {\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }} \cr & C{o^{3 + }} = 1{s^2}\,2{s^2}\,2{p^6}\,3{s^2}\,3{p^6}\,3{d^6} \cr} $$
$$C{N^ - }$$ is a strong field ligand and as it approaches the metal ion, the electrons must pair up.
The splitting of the $$d$$ - orbitals into two sets of orbitals in an octahedral $${\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ may be represented as

Here, for $${d^6}\,ions,$$ three electrons first enter orbitals with parallel spin put the remaining may pair up in $${t_{2g}}$$ orbital giving rise to low spin complex ( strong ligand ) field.
$$\therefore \,\,{\left[ {Co{{\left( {CN} \right)}_6}} \right]^{3 - }}$$ has no unpaired electron and will be in a low spin configuration.