Question
Which of the following has more unpaired $$d$$-electrons?
A.
$$Z{n^ + }$$
B.
$$F{e^{2 + }}$$
C.
$${N^{3 + }}$$
D.
$$C{u^ + }$$
Answer :
$$F{e^{2 + }}$$
Solution :
$$Z{n^ + }\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 30} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^{10}},4{s^1}$$
(no unpaired $$d$$-electrons)
$$F{e^{2 + }}\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 26} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^6}$$
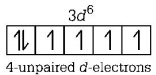
$${N^{3 + }}\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 7} \right) = 1{s^2},2{s^2}2{p^0}$$
(no unpaired $$d$$-electrons)
$$C{u^ + }\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 29} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^{10}}$$
(no unpaired $$d$$-electrons)
So, maximum number of unpaired electrons are present in $$F{e^{2 + }}.$$
$$Z{n^ + }\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 30} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^{10}},4{s^1}$$
(no unpaired $$d$$-electrons)
$$F{e^{2 + }}\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 26} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^6}$$

$${N^{3 + }}\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 7} \right) = 1{s^2},2{s^2}2{p^0}$$
(no unpaired $$d$$-electrons)
$$C{u^ + }\left( {{\text{at}}{\text{.}}\,{\text{no}}{\text{.}} = 29} \right) = 1{s^2},2{s^2}2{p^6},$$ $$3{s^2}3{p^6}3{d^{10}}$$
(no unpaired $$d$$-electrons)
So, maximum number of unpaired electrons are present in $$F{e^{2 + }}.$$